Setting the Student Up for Success
As a math teacher who works with students from kindergarten through fifth grade daily, I recognize the struggle students have with retaining math concepts, even ones that began in kindergarten. The need to reteach lessons and fill in missing gaps can be overwhelming. Once we move on to a new unit or topic, it was as if everything we just worked on (for what felt like forever!) just vanished out of their minds.
The beginning of many children’s mathematical careers is in kindergarten, when they first learn how to count. They begin by memorizing the numbers, then use number recognition to correctly order them. Then they can count objects by using one-to-one correspondence and understanding one more and one less.
In this way, counting is partly putting numbers together, that is putting numbers into a basic structure that can be used across all of math. As students advance, they will continue to build upon their knowledge of numbers and learn that just as important as putting numbers together is the ability to break numbers apart.
Breaking Numbers Apart in Mathematics
Basics of Breaking Numbers Apart (Grades K–2)
Before we can jump into the concept of place value, we need to establish an understanding of the number 10 and how to break it apart.
Key Standards:
- Write numbers up to 5 as a sum of two integers (Grade K)
- Fluently add and subtract within 10 (Grade 1)
- Add and subtract within 20 (Grade 2)
A kindergarten student will first begin with breaking apart the number 5, at this age it is done using a concrete model. My go-to activity is pulling out the connecting cubes and giving each student 5.

I always allow my students to have a moment to look over and inspect their manipulative. Once they have done so, I would ask them how many cubes they have all together, and hopefully their answer will be 5. Next, I will walk them through various situations where they will realize that no matter how we separate the 5 cubes, they will always have a total of 5 cubes at the end.

The next progression would be introducing 10 connecting cubes, sticking with the same mindset that no matter how you break apart the number 10, you will always have the total of 10. As you continue to work with larger numbers, you can take away the manipulatives and use more visual representations like a math mountain, as it’s referred to in Math Expressions. A math mountain breaks numbers up into a representation where the “peak” is the sum and the “base” is made up the addends. It introduces the concept that addition and subtraction are related—or connected—and the numbers they choose will always be the same.
Example: A student breaks 10 into 4 and 6 then sees that 4 + 6 = 10. Then, you can introduce the related equations 10 – 4 = 6 and 10 – 6 = 4.

Breaking Apart by Place Value (Grades 2–3)
Second grade is when we really take a deeper dive into the importance of the number 10 and the concept of place value.
Key Standards:
- Understand place value up to 1,000 (Grade 2)
- Read and write numbers to 1,000 in expanded form (Grade 2)
- Fluently add and subtract within 1,000 (Grade 3)
This is where we introduce students to the process of breaking down numbers and writing them in expanded form. Writing a number in expanded form is the process of breaking a number apart based off place value. For example, the number 472 in expanded form is 400 + 70 + 2.
After students break a number down into its place values, ask them how they came up with their expressions. Call attention to similarities and differences in the explanations that students provide and ensure that all students understand the main idea that when you break down 472, you have 4 hundreds, 7 tens, and 2 ones.
When teaching this concept, my goal is to expand my students’ thinking and see if they truly do understand that expanded form is just breaking a number apart according to its place value. Will they still grasp that concept if a number written in expanded form isn’t written out in the correct place value order? To assess my students’ understanding, I will give them a number in expanded form but out of order, such as 20 + 8 + 600, then ask them to write it in standard form.
The number in standard form is 628; however, often I’ll see student responses like 208,600 or 286. These are common mistakes where the student will forget the concept of breaking the number apart based on place value and will instead only pay attention to the order that the numbers are written in. One scaffold I use in these instances is providing a place value chart. This allows students to organize and visualize breaking the number apart.
Example 1: Rewrite the number 2,436 in expanded form.
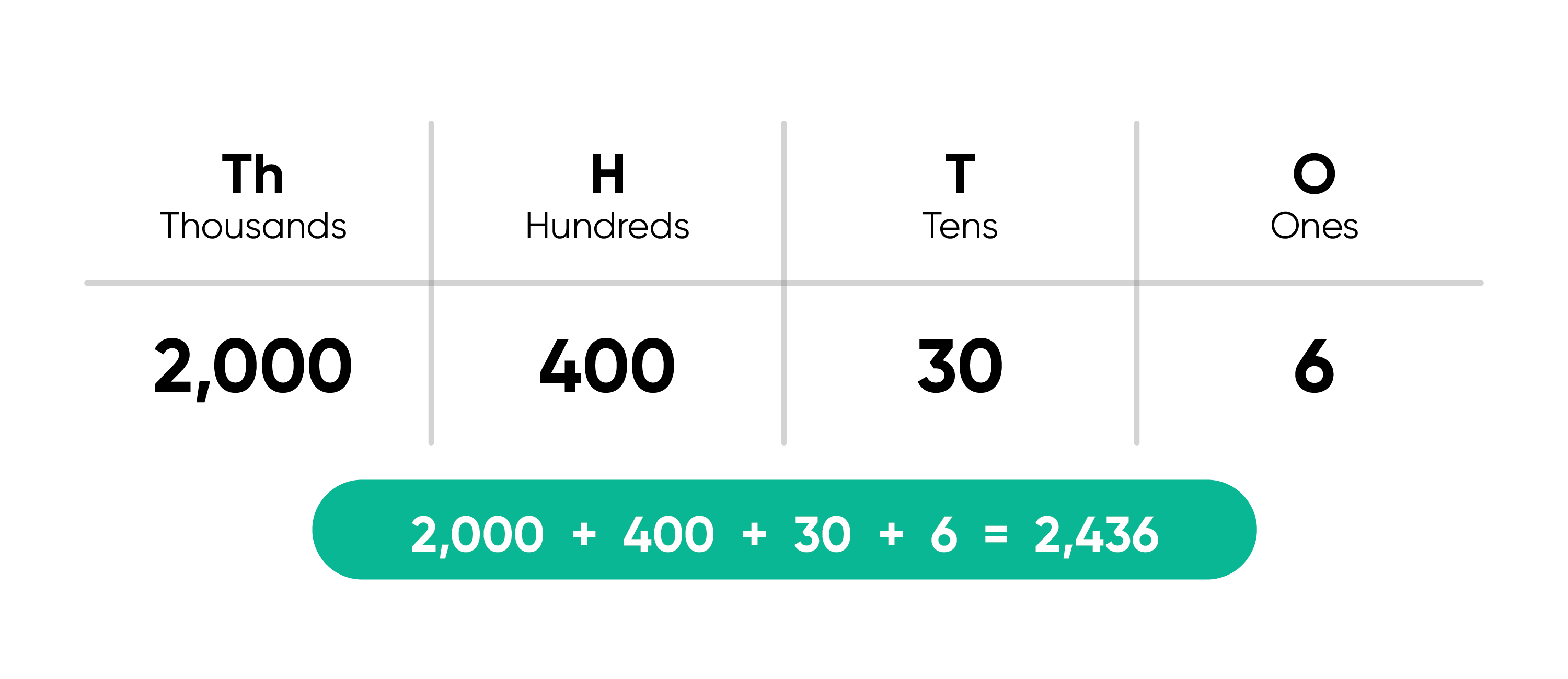
For the next example, encourage students who are stuck to organize the given numbers into their correct place on a place value chart.
Example 2: Rewrite the number 70 + 3,000 + 1 + 100 in standard form.

When students are able to break numbers apart by place value, it helps them understand how to add large numbers. For example, the sum 485 + 238 can be thought of as adding 4 hundreds + 2 hundreds, 8 tens + 3 tens, and 5 ones + 8 ones. For help visualizing these concepts, try using ones cubes, tens sticks, and hundreds squares.
Breaking Apart into Factors (Grades 3–5)
Following addition and subtraction, students begin to work with the next two operations: multiplication and division.
Key Standards:
- Represent and solve multiplication and division problems (Grade 3)
- Understand the relationship between multiplication and division (Grade 4)
- Understand the place value system (Grade 5)
The teaching of multiplication and division all starts with evaluating the numbers and breaking them apart. For example, when teaching a student, the concept of multiplication begins with an equation. Let’s say we are finding the product of 4 × 3. We would create a visual representation of 4 groups of 3 objects.
The same method can be used for division. If you have 20 ÷ 4, the language will remain the same by saying, “how many groups of 4 can go into 20?” Using a visual representation, a student could create 4 groups and discover that they get 4 groups of 5.

Most numbers do not divide evenly into one another, however. But even then, remainders are another way to think about breaking numbers apart. When dividing 23 by 5, for example, 23 is being broken into 5 groups of 4 with a remainder of 3. This concept of breaking a number into uneven parts can be expressed with a fraction:
\[23 \div 5 = 4\frac{3}{5}\]
The reason that the remainder can be expressed as a fraction is because there wasn’t enough to make another full group of 5, there were 3 parts remaining. A fraction is a number that doesn’t represent a whole quantity, it is a part or a portion of a whole. Fractions are another example of how a number can be broken apart. Benchmark fractions are introduced in 3rd and 4th grade, these fractions include \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\), \(\frac{1}{5}\), \(\frac{1}{6}\), \(\frac{1}{8}\), \(\frac{1}{10}\), and \(\frac{1}{12}\). When teaching fractions, be sure to point out that the fraction is a number less than one. Eventually, you will use these benchmark fractions and concepts of fractions to teach decimals.
Extending the Math: All the Ways to Break a Number Apart
The basic principles above extend all throughout mathematics, at the elementary level and beyond. Utilizing place value will continue to help students break apart numbers when solving problems using the 4 arithmetic operations (addition, subtraction, multiplication, and division).
The concept of breaking numbers apart can extend to secondary mathematics and beyond, as well. At the secondary level, the importance of the powers of 10 and how it relates to place value system should be known. The connection that our numerical system works by the powers of 10s and how they are represented by both positive and negative exponents, \(10^1\), \(10^2\), \(10^3\),... and \(10^{-1}\), \(10^{-2}\), \(10^{-3}\),....
A deeper understanding of breaking a number apart will in return help when solving more complex mathematical problems. Whether they are in algebra or trigonometry class, creating a budget for college, or looking to buy a home. There will never be a shortage of situations where math is needed to solve a problem.
Lessons and Activities on Breaking Numbers Apart
Take a look at some of the lessons and activities we’ve compiled to help you teach the concept of breaking numbers apart to your students:
- Math Activities for Preschoolers: Discovering Addition Concepts (Grades PreK–K)
- Teaching with Math Place-Value Charts (Grades 1–2)
- Grade 2 Math Activity Set: By the Sea and A Bunch of Animals (Grade 2)
- Teaching Multiplication and Division Relationship Using Arrays (Grades 3–4)
- Teaching Product of Prime Factors (Grades 4–6)
- Teaching Prime Factorization of 36 (Grades 4–6)
- Teaching Dividend, Divisor, and Quotient in Division (Grades 4–6)
- Factor in Fun! 3 Factor Games for the Classroom (Grades 5 and up)
***
Looking for a math curriculum that will grow student confidence in mathematics and help learners master breaking numbers apart? Explore our core math solution HMH Into Math for Grades K–8.
Get our FREE guide "Optimizing the Math Classroom: 6 Best Practices."












