
Coordinate graphing can sound very daunting for students in Grades 4–9, but it's actually just a visual method for showing relationships between numbers. The relationships are shown on a coordinate grid. A coordinate grid has two perpendicular lines, or axes (pronounced AX-eez), labeled just like number lines. The horizontal axis is usually called the x-axis. The vertical axis is usually called the y-axis. The point where the x- and y-axis intersect is called the origin.
Drawing a Coordinate Graph
The numbers on a coordinate grid are used to locate points. Each point can be identified by an ordered pair of numbers; that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate. Ordered pairs are written in parentheses (x-coordinate, y-coordinate). The origin is located at (0,0). Note that coordinates are often written with no space after the comma.
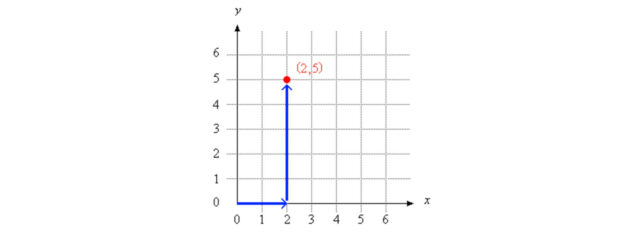
The location of (2,5) is shown on the coordinate grid below. The x-coordinate is 2. The y-coordinate is 5. To locate (2,5), move 2 units to the right on the x-axis and 5 units up on the y-axis.
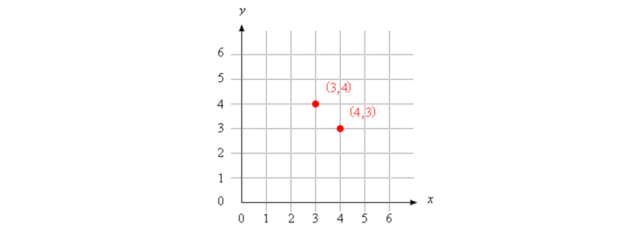
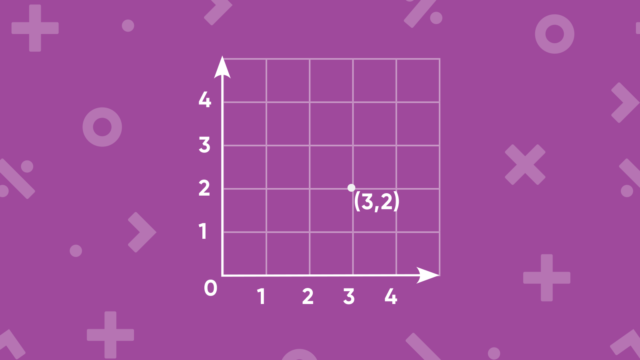
The order in which you write x- and y-coordinates in an ordered pair is very important. The x-coordinate always comes first, followed by the y-coordinate. As you can see in the coordinate grid below, the ordered pairs (3,4) and (4,3) are two different points!
Describing a Linear Relationship
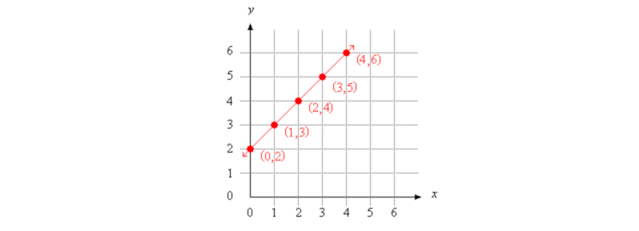
The function table below shows the x- and y-coordinates for five ordered pairs. You can describe the relationship between the x- and y-coordinates for each of these ordered pairs with this rule: the x-coordinate plus two equals the y-coordinate. You can also describe this relationship with the algebraic equation x + 2 = y.
| x-coordinate | x + 2 = y | y-coordinate | ordered pair |
| 0 | 0 + 2 = 2 | 2 | (0,2) |
| 1 | 1 + 2 = 3 | 3 | (1,3) |
| 2 | 2 + 2 = 4 | 4 | (2,4) |
| 3 | 3 + 2 = 5 | 5 | (3,5) |
| 4 | 4 + 2 = 6 | 6 | (4,6) |
To graph the equation x + 2 = y, each ordered pair is located on a coordinate grid, then the points are connected. In fact, the graph forms a straight line. The arrows indicate that the line goes on in both directions.
For students who are ready to take it to the next level, consider explaining that the graph for any equation that can be written as ax + by = c, where a, b, and c are numbers, forms a straight line. Notice how x + 2 = y can also be written as ax + by = c, where a = 1, b = –1, and c = –2.
Introducing the Concept
Finding and Graphing Points for Linear Relationships
Your students may have encountered ordered pairs last year, but it's a good idea to start by reviewing how to locate a point on a grid from an ordered pair. A day spent plotting coordinates that fall in a straight line will be a day well spent.
Key Standard: Graph points on the coordinate plane. (5.G.A.1)
Materials: Poster paper or a way to display a coordinate grid publicly for the class; straightedge
Preparation: Draw a large coordinate grid that the entire class can see. Label the x- and y-axes from 0 through 10.
Prerequisite Skills and Concepts: Students should know about ordered pairs and locating points on a grid.
- Write these ordered pairs where all students can see them: (6,4); (7,5); (8,6); and (9,7). Point to the ordered pair (6,4).
- Ask: What rule describes the relationship between the numbers in this ordered pair?
Although many rules work for this pair in isolation, elicit from students this rule: the first number minus two equals the second number. - Ask: Does the same rule apply to the other ordered pairs?
Students should notice that each ordered pair follows this rule. You can help them by using the rule to write each ordered pair as an equation: 6 – 2 = 4, 7 – 2 = 5, 8 – 2 = 6, 9 – 2 = 7. - Say: Let's locate these ordered pairs on a grid.
- Ask: How would you locate the point for (6,4) on the grid?
Students should say to "start at 0, move 6 units to the right, then 4 units up." Mark this point on the grid for the class to see. - Have students verbalize how to locate the point for each of the other ordered pairs. Then mark each point on the grid. Emphasize the importance of moving right for the first number in the ordered pair and up for the second number.
- Ask: What figure do you think will be formed by connecting the points on the grid?
Students should see that a line will be formed. Use a straightedge to connect the points. - Provide students with other examples of ordered pairs that follow a rule. Have students identify the rule and explain how to graph the points. One example could read, "Rule: The first number plus three equals the second number; ordered pairs: (2,5); (3,6); (4,7); and (5,8)."
Developing the Concept
Finding and Graphing Points for Linear Relationships
At this level, students will begin to see the relationship between equations and straight-line graphs on a coordinate grid.
Key Standard: Interpret an equation as a linear function, whose graph is a straight line. (8.F.A.3)
Materials: Poster paper or a way to display a coordinate grid publicly for the class; straightedge; one copy of a coordinate grid, a straightedge, and lined paper for each student
Preparation: Draw a coordinate grid where all students can see it. Label the x- and y-axes from 0 through 10. Ensure all students have a copy of the grid.
Prerequisite Skills and Concepts: Students should know about ordered pairs and locating points on a grid. They should also be able to recognize and interpret an equation.
- Write the equation x + 5 = y publicly for the class to see.
- Ask: How could you say this equation in words?
Students should say that the equation means "a number plus five equals another number," or a comparable statement. - Draw a table with four columns and five rows. Have students draw their own table. Label the first column x, the second column x + 5, and the third column y. Leave the fourth column blank for now. Write "1" in the first column below x.
- Ask: What happens to the equation if we replace x with 1? Elicit from students the equation 1 + 5 = 6. Write "1 + 5" in the second column below "x + 5." Then write "6" in the third column below y.
- Continue to replace x with 2, 3, then 4. Have students complete the first three columns of their tables on their own. Then ask for a volunteer to complete the table publicly for the class.
- Say: Let's write ordered pairs using the values of x and y. Label the fourth column of your table "Ordered Pairs." Remind students that when they locate points on a grid, they first move right on the x-axis, then up on the y-axis. Therefore, the first number in an ordered pair is a value for x, and the second number is a value for y. These numbers are called the x- and y-coordinates.
- Ask: What is the first number we used for x? (1) What is the first number we calculated for y? (6) So, what is the first ordered pair? (1,6)
Have students complete their tables. When they are finished, record the ordered pairs in the table publicly for the class. - Say: Now we're going to graph the equation x + 5 = y on a grid. (Point to the grid you made.) This grid is called a coordinate grid. Let's take a closer look at the different parts of the grid.
- Point to the horizontal line on the grid.
- Say: This line is called the x-axis.
- Point to the vertical line on the grid.
- Ask: What do you think this line is called?
Students should make the connection to the y-axis. - Say: Now, let's locate the ordered pairs on the grid. Who can find (1,6)?
Have a volunteer describe the location of the ordered pair. Mark the location on the coordinate grid for all students to see. Then have students locate the rest of the ordered pairs on their own grids. - Say: Let's connect all of the points. What figure did we make?
Have students use a straight edge to connect the points. Show students how extending both ends of the line slightly, and drawing arrows, shows that the line goes on in both directions. Students should identify the figure as a straight line. - Have students repeat this activity with the equation x – 2 = y. Use the numbers 5, 6, 7, 8, and 9 for x.
Wrap-Up and Assessment Hints
These skills will need lots of practice. Reinforce the need for students to work carefully so their graph is accurate. When you assess students' progress, keep the number of exercises small enough that they have time to complete each step without rushing.
This blog post, originally published in 2020, has been updated for 2021.
With this math lesson, you can teach students about coordinates, integers, coordinate planes, and functions on a graph.

Try these free middle school math activities that cover budgeting, taxes, social media engagement, coding, and many more topics.
Here's a helpful list of healthy habits to enable a growth mindset in math, plus a free downloadable poster for your classroom.
Get our FREE guide "Optimizing the Math Classroom: 6 Best Practices."












