Big and Little
 All Classroom Lessons
All Classroom Lessons
A Lesson for Third Grade

by Jamee Petersen
Understanding the concept of scale is not easy for young children, but Steve Jenkins’s book Big and Little (Houghton Mifflin, 1996) can help. The illustrations in the book show animals at the same scale, making it easy to compare their sizes visually. In this lesson, Jamee Petersen uses the book to introduce third graders to the idea that a 1-inch illustration can represent 8 inches in the real world. Jamee’s forthcoming book, Math and Nonfiction, Grades K–2, will be published by Math Solutions Publications in fall 2004; in her new book, she includes a lesson about how to use Big and Little with kindergarten children.
When I read Big and Little to a class of third graders, I began with Steve Jenkins’s note to his readers in which he explains that all of the animals in the book “are related but different in size.” After explaining a bit more about this, Jenkins writes, “All of the creatures in this book are illustrated at the same scale (one inch equals eight inches) so animals throughout the book can be compared.”
After reading the book through once, I said to the class, “You know, we have examples of big and little right here in this room. How many of you know how tall you are?”
Some students knew an exact measurement. Emma said, “I am three feet and ten inches.” Others gave a relative measurement. Alison said, “I know I’m taller than Jack but shorter than Hannah.”
“Remember the author’s message at the beginning of Big and Little?” I asked the class. “Some of animals in this book are too big for the author to show as their actual size, but because he wanted us to be able to compare their sizes, he made a scale. The animals in this book are all drawn so that one inch in the drawing equals eight inches in the real world. That was his scale.” On the board I wrote:
1 inch (in the book) = 8 inches (in the real world)
“What do you think this means?” I asked.
“It means that you times it by eight,” Alan said.
“It means that if an animal is exactly eight inches tall, then it is one inch tall in this book,” Carrie said proudly.
Max agreed but explained it in this way after getting a ruler: “It means that one inch in the book,” and he covered up the ruler with his arm so that only 1 inch showed, “really equals eight inches.” Max then moved his arm so that 8 inches showed.
While some students seemed to grasp this concept, I knew that others didn’t. I suggested we “test” Max’s idea on the illustration of the Siamese cat shown sitting on the book’s first page. Knowing all the students would have a good idea of the size of a house cat, I took Max’s ruler and carefully laid it next to the cat in the book.
A few students in the front helped read the measurement, explaining that the cat was more than 1 but less than 2 inches. “The cat is one and a half inches tall,” Aaron announced to the rest of the class.
“So if the illustration of the cat is one and a half inches tall and we know that one inch equals eight inches, then how tall is the cat in real life?” I asked.
To solve this problem, some students went to get rulers while others sat thinking quietly. After a few moments, I called them all to attention and said, “I’m interested in knowing how you thought about solving this problem.” Many hands went up.
Jose said, “Well, the cat is one and a half inches. One inch is eight inches and I know that half of eight is four, so the real cat is twelve inches tall.”
Kara said, “I knew my doubles. And halves and doubles are kind of the same thing, so I just said eight and then half of eight is four and eight plus four equals twelve. So the cat is twelve and that seems right.” Kara placed her hand about 12 inches from the floor and added, “This is about how high my cat is when he’s sitting.”
Some hands went down, indicating to me that those students had thought about the problem in a similar way. Still others were still waving wildly.
“I did it different,” Sara said. “I took the ruler and found eight because I knew the cat was one whole inch and one inch is eight. Then I looked at the ruler and I just saw that four was half of eight so I just moved my hand up like this,” Sara explained, as she deliberately moved her hand up the ruler, counting on four more from the 8. “So that’s when I saw it was twelve inches,” she concluded.
“Twelve inches is a foot, so the answer could be one foot tall,” surmised Justin.
“So we figured out how tall the cat in the book would be in real life; is there a way we could figure out how tall you would be if you were in this book?” I asked.
The students first looked puzzled but then began to smile as they anticipated the activity. “Yeah, we would just need to figure how tall we are and then go back by eight,” Carrie said. “Tell me more,” I asked.
“Well, it’s the same way we figure out the cat but in reverse,” Carrie added.
I asked Kathy to come to the front of the room to help me. She came up and stood in front of the others. “I would need to measure Kathy’s height first,” I said. First I had other children help by holding rulers, one on top of the other, but then I suggested that maybe another measuring tool would work better. Some wanted to use a yardstick, with Kathy lying down; others thought a measuring tape would be best.
I tried all of their suggestions, modeling many ways to measure and purposefully demonstrating common mistakes, such as not having the tape tight or leaving spaces between the rulers rather than having them touch. We found out that Kathy was just over 50 inches tall.
“OK, Kathy is about fifty inches tall,” I said, rounding to the nearest inch. “How can we fig- ure out how tall a drawing of Kathy should be if we used the scale of one inch equals eight inches?” I gestured to the board where I had earlier written 1 inch (in the book) = 8 inches (in the real world).
I was surprised at how many hands shot up. “We would have to find out how many eights are in fifty,” Jose offered.
“Yes, that’s right,” I said. At this point, I explained to the children that their task was to figure out how little they would be if they were illustrated in the book Big and Little. “You may use any tools you think would help you. You may work in teams to help each other get an accurate measurement, but I’d like each of you to have a written record of what you did. Your paper should help others understand your thinking. Your explanation may have words, numbers, and a picture—whatever you think will help explain your thinking.” I placed some white drawing paper out for the students to record their thinking and they got to work.

Figure 1. Nathan used a ruler to help solve the problem.
Nathan decided working with segments of 8 inches would be easiest. I understood how he came up with the 6 in his answer but the 11/24 puzzled me. When I asked Nathan about his answer, he explained, “I got eleven–twenty-fourths because there were six rulers and then there was five and a half of the next one; five and a half of twelve inches, so I added on eleven– twenty-fourths. So I had six and eleven–twenty-fourths.” Nathan’s reasoning wasn’t accurate, but I was impressed that a student his age was comfortable enough in his number sense and reasoning skills to attempt converting a mixed number into a fraction.
When I looked at Alex’s work, I could see he had erased 53 and changed it to 52. I asked him to explain. He said, “I went down to fifty-two because it’s an even number and I usually work better with even numbers.”

Figure 2. Alex’s work with division.
Molly’s and Marie’s papers were similar. Both girls grouped by eight, one using number symbols and repeated addition and the other using tally marks in groups of eight.
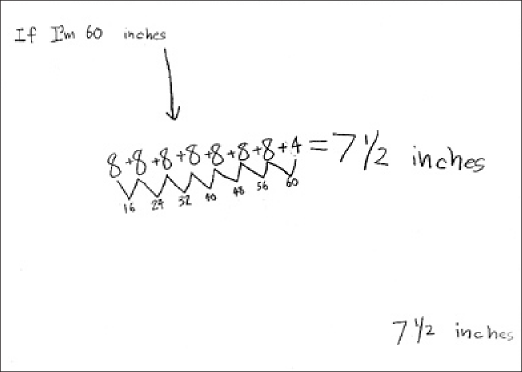
Figure 3. Molly recorded her work as repeated addition and then counted by eights.

Figure 4. Marie used a grouping model.
The next day I read Big and Little once more to my students. Before reading, I asked them to use their work from the previous day to create simple drawings of themselves using their “book heights” based on the scale of 1 inch being equal to 8 inches. They cut out their drawings and brought them to the rug with them as they gathered for the story. As I read, students were able to compare their heights with the heights of animals included in the book. Placing their drawing cut out next to the big tiger and the little hummingbird brought an even greater depth of understanding of the different sizes of these animals.
From Online Newsletter Issue Number 14, Summer 2004

Comments