The fourth graders I’ve been working with had been studying fractions for about a week before I taught this lesson. They were using fraction pieces that they’d each cut for a beginning set of fractions—1 whole, 1/2, 1/4, 1/8, and 1/16. Magnetic versions of their fraction pieces were especially useful for this lesson. (Information about these Fraction Kits appears at the end of the blog.)
To prepare for the lesson, I cut a length of string about a yard and a half long and tied four knots in it, spacing them 15 inches apart. I chose this distance between knots to match the length of the blue whole strip they each had and the magnetic whole strip I had.
I talked with the class about how knotted strings were used as early measuring tools, before we had rulers and tape measures. I taped the string on the board and asked them to think about it as a number line. I labeled the knots 0, 1, 2, and 3.
Then I asked the students to watch as I moved my finger along the string from the point marked 0 to the point marked 1. I said, “Tell me to stop when you think I’m halfway between these two knots, halfway between zero and one.” I moved my finger slowly, tracing the string, until they shouted, “Stop!”

We checked with the red 1/2 strip to confirm. When I asked them how I could label this point, they said it was 1/2. I wrote 1/2 on the board under the point..
Then I did the same to locate a point halfway between 0 and 1/2. We checked the distance from zero to the point with the one-fourth fraction piece, and I labeled the point 1/4. I repeated to label 3/4 and 1 1/2.
I then said something like, “So here I used fractions to label points on a number line, just as we used zero, one, two, and three. So I think we can say that fractions are also numbers.” I’m not sure they all were completely convinced, but there were nods and no rebuttals.
Next I talked with them about different names for the same fractions. I reminded them that they call me “Ms. Burns” but that some people call me “Marilyn.” We talked about other fractions we could use as labels for 1/2. As students made suggestions, I listed them on the board under 1/2 on the number line and verified them when possible with fraction pieces.
Then I wrote 50/100 on the list, for which we didn’t have fraction pieces. The students seemed clear that it was equal to 1/2. They offered other fractions that they thought were also equal to 1/2, and I added them to the list. I asked them to talk with a partner and come up with a statement that explains how you’d know by looking at a fraction if it was another label for 1/2.
There were two views. Jaleya said, “A fraction is equal to one-half if two times the numerator equals the denominator.” (Actually this was her third iteration—she stumbled a few times and each time I asked her to try again until she could deliver her thought clearly.) Alisha had a different view. She said, “A fraction is the same as one-half if you can add the numerator to itself and that gives the denominator.”
I then asked them for different numbers we could write as labels for 1, and then for 1 1/2.

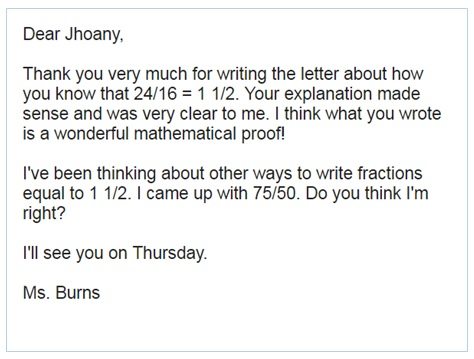
When Jhoany offered 24/16 for 1 1/2, most of the students seemed confused. I wrote Jhoany’s suggestion on the board as a conjecture to return to at another time. I did this to give his classmates time to think about his idea.

The day after the lesson, on a prompt from Sara, his regular teacher, Jhoany wrote a letter to me about why he thought 24/16 was equal to 1/2. Here’s what he wrote:

I’m not in class every day, so I sent Sara a response for her to share with Jhoany. I’m curious about how he responds. Stay tuned!
Learning about fractions, as with all new ideas, takes time. Students benefit from exploring with concrete materials, having experiences to express how they are reasoning, and listening to the ideas of others. They need time to revise, cement, and extend their thinking. I plan to return to this experience with fractions on a number line as the students learn more about comparing and ordering fractions.
About the Fraction Kit
The Fraction Kit is the single most effective manipulative material that I rely on for teaching fractions. It’s been a mainstay of my teaching repertoire for years and I’ve used it with students in grades 3 through 8, in whole-class instruction and in small groups when providing intervention. The Fraction Kit is featured in various of my resources—including About Teaching Mathematics (p. 422–426), Do The Math in Fractions A, B, and C; and Teaching Arithmetic: Lessons for Introducing Fractions. It’s possible to cut the fraction strips from construction paper and make the number cubes for the games, but it’s also possible to purchase a Fraction Kit that has materials for 30 students.

 All Blog Posts
All Blog Posts
Comments