In my early years teaching mathematics, I taught students to compare fractions the way I had learned as an elementary student—convert the fractions so they all have common denominators. However, in my more recent teaching of fractions, I do not teach one method. Instead, I prod students to think, reason, and make sense of comparing fractions, helping them learn a variety of strategies that they can apply appropriately in different situations. While changing fractions so that they have common denominators is one useful strategy, it’s not the only nor most efficient one.
To help students learn to compare fractions, I used several types of lessons. I gave students real-world problems to solve, such as sharing cookies or comparing how much pizza different people ate, and had class discussions about different ways to solve the problems. I gave them experiences with manipulative materials—pattern blocks, color tiles, Cuisenaire rods, and others—and we explored and discussed how to represent fractional parts. I taught fraction games that required them to compare fractions, and we shared strategies. At times I just gave them fractions, and we discussed different ways to compare them.
We talked a good deal about fractions. By expressing their own ideas and hearing ideas from others, children expand their views of how to think mathematically. Also, talking and listen- ing helps prepare them for writing, which I have them do individually several times a week in class and often for homework as well. My students had many opportunities to explain in writing how they compared fractions.
I began one class lesson by asking the students to think about two fractions—6/8 and 4/5. “Which is larger?” I asked them. “And how did you decide?” On this day I didn’t have them discuss their ideas but instead asked them to write individually so that I could see how each student thought. (How would you decide which of the two fractions is larger?)
The students’ papers showed a variety of methods. Laura wrote: 6/8 < 4/5 because 6/8 = 12/16 and 4/5 = 12/15 and you have the same numerator so it makes it easier in a way. 12/15 is bigger than 12/16 so 4/5 is bigger than 6/8. I wasn’t sure from my first reading how Laura was thinking.
This is common when I read student work. It’s hard to follow others’ reasoning, especially when their thinking differs from ours. I read Laura’s explanation again and realized that she had converted the fractions so that they had common numerators. She didn’t explain how she knew that 12/15 was larger than 12/16; that seemed to be obvious to her. But her method worked and was efficient.
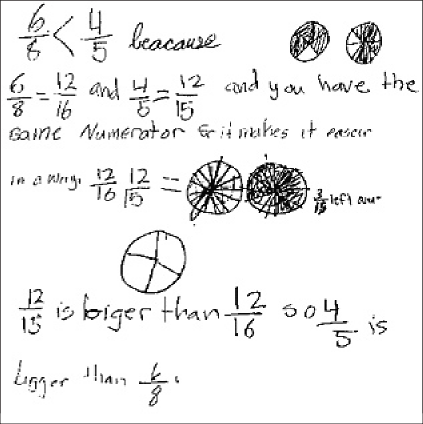
I read Brian’s paper next. He had reasoned the same way that Laura had but expressed his thinking differently and with more detail. He wrote: I know that 6/8 is = to 12/16 because 6 x 2 = 12 and 8 x 2 = 16. 4/5 = to 12/15 because 4 x 3 = 12 and 5 x 3 = 15. 16 is a bigger number but a smaller fraction and 15 is a smaller number but a bigger fraction witch makes 6/8 = 12/16 , 4/5 = 12/15. While Brian’s language wasn’t precise, it indicated that he understood that the larger the denominator, the smaller the fractional pieces. Brian’s paper was easier for me to understand, mostly I think because I had reasoned through Laura’s paper first.
Jenny, however, reasoned differently. She compared both fractions to one whole. She wrote: 6/8 is less than 4/5 because 6/8 is 2/8 away from 1 whole and 4/5 is 1/5 away from the whole. 2/8 is equal to 1/4. 1/4 is bigger than 1/5 so 4/5 is bigger than 6/8 because it has a smaller amount left to get to the whole. Jenny’s method also shows her understanding of equivalent fractions, that 2/8 is the same as 1/4. Jenny’s explanation was clear and correct. Also, it was easy for me to understand because her approach mirrored the way I had thought about the problem.

As Jenny did, Donald compared both fractions to one whole and showed his understanding of equivalent fractions. But he also thought about common numerators. He wrote: I know that 6/8 is less than 4/5 because 4/5 = 8/10 which is 2/10 away from the whole. And 6/8 is 2/8 away from the whole. And 8/10 is more than 6/8 because 10’s are smaller than 8’s which would make it closer a whole which make it more. Donald’s explanation had some grammatical errors. He meant “10ths” and “8ths,” not 10’s and 8’s. His use of “it” twice weakened the last sentence, and he left out the word “to” where it needed to be. The sentence would have been clearer if Donald had written:
And 8/10 is more than 6/8 because 10ths are smaller than 8ths, which would make 8/10 closer to a whole, which makes it more. Donald needed to be reminded regularly to reread his papers before handing them in, and although this paper represented an improvement in his writing, more improvement was still needed.
Mariah relied on common denominators. She wrote: I know that 6/8 < 4/5 because I know that 6/8 also = 30/40 and 4/5 also = 32/40 and 30/40 is less than 32/40 so 4/5 > 6/8. 30/40 is 2/40 away from 32/40. I got this because I used common denominators. Mariah also showed how she had arrived at the converted fractions. She wrote:
4/5 8/10 12/15 16/20 20/25 24/30 28/35 32/40
6/8 12/16 18/24 24/32 30/40
All of these students’ answers were correct and their explanations acceptable. They were doing what made sense to them as they tried to reason about the fractions.
Using Student Writing in the Classroom
After reading through the students’ papers, I have discussions with individuals, especially if I’m having difficulty understanding their reasoning or if their reasoning was incorrect or incomplete. Sometimes I focus on their writing errors; other times I keep the focus just on the mathematics. Making this decision depends on the paper, the student, and the mathematics involved.
Then I have some students share their papers with the class so that students can benefit from one another’s thinking. For example, I asked Mariah to show the class how she arrived at fractions with common denominators. Her method wasn’t conventional, but it was mathematically correct and effective. She explained, “I kept changing them to equal fractions. I knew when I hit fortieths that it would work for six-eighths.”
Mariah’s explanation sparked a class discussion about other ways to convert fractions to ones with common denominators. Several students were eager to explain the methods they used. Raul was particularly animated. He said, “If you multiply 8 times 5 you get 40 and you can use that as the denominator. Then multiply 6 times 5 to get 30 and have that numerator for six- eighths and then multiply 4 times 8 and use 32 for the numerator for four-fifths.”
Mariah nodded, seeming to understand. “But I like my way better,” she said softly.
“It’s okay for you to use your own method,” I responded. “It’s also important that you learn different ways to think about fractions.” (I constantly remind children to look at many different strategies to develop and extend their mathematical repertoire.) Then I wrote two fractions on the board—3/4 and 2/3—and asked each student to take out a sheet of paper and convert these to common denominators in two ways – Mariah’s way and Raul’s way. I had them compare their work with partners and then had volunteers demonstrate each method so that Mariah and Raul could judge if their methods had been correctly applied.
I had others read their papers as well and began to compile a class list of strategies for comparing fractions. I acknowledged students’ ideas—Mariah’s way, Brian’s way, and so on—and then gave the strategies general names—convert to common denominators, see which is closer to 1, convert to common numerators, etc. I wrote the list on chart paper and kept it posted in the classroom for students to refer to.
In my years of teaching, not all classes have come up with all strategies. (This was the first class in which common numerators was such a prevalent strategy.) If there’s a strategy that I want students to know about and no one presents it, then I present and provide practice with it. But I present it as one of many, not as the “best” or “right” way to compare fractions. The “best” or “right” way depends on the context, the numbers, the purpose, or some combination of these factors.
A Suggestion for Your Classroom
You might try sharing one of my students’ methods with your class. Reproduce one of them, give copies to students in pairs, and have them see if they can figure out why it makes sense. Have them explain the method in their own words. Then give them practice applying it to other fractions. In this way, you can use the work of some of my students to help develop your own students’ skills and understanding. But, if possible, share the ideas from your own class. Honoring your students’ thinking is a way to involve them as important contributors to their learning and to the learning of their classmates.
This blog post originally appeared in Newsletter Issue Number 24.

 All Blog Posts
All Blog Posts
Comments