Subitizing! This ability to instantly “see” how many is a critical component in young students developing number sense. There are two types:
1. Perceptual subitizing—the ability to see a small number of objects and know how many there are without counting. For example, this skill allows us to realize we “rolled six” on a die without counting. It is usually an instantaneous realization, and generally applies to small amounts of objects.
2. Conceptual subitizing—the ability to see more than one group and add them together to find the total. This one takes a little more effort as it requires recognizing smaller groups and adding them up.
Studies cite the use of subitizing in primary grades as the key to students being able to pass algebra. It builds the skills needed to move toward proficiency in a sense of equality and balanced equations, spatial sense, and number sense. We know subitizing is an important part of building procedural fluency through conceptual understanding, but how do we prepare students for this?
Students need tangible experience working with number sets—and if we can create a tangible experience that is also FUN, success will come much more quickly. A common strategy is to work with dot arrangements, but any simple symbol can be used, such as stars or squares. To add the fun factor, I expanded on an idea from my colleague, Mary Gong, who used spaceships in her primary classroom. Her “spaceships” were nothing more than paper plates with large dots made with stickers or Bingo dauber, but were effective nonetheless. You can get as creative as you like here but be sure to stick with simple shapes and vary the patterns on each. First, I randomly provided students with paper plates with small sets of 3–5 stars. I asked them to silently maneuver their “spaceships” to another student with a matching number of dots. I then led a discussion, using the prompt, “How did you know the set has the same number when it looks different?”
After this activity, I placed students in two groups to explore more concepts. I asked Group 1 to “fly” to a student in Group 2 with a spaceship that had fewer dots than their own. Then, I asked Group 2 to fly to a student in Group 1 with a spaceship that had more dots. I also had each student hunt for a copilot, whose spaceship combined with his/her own, totaled a certain number. You can easily do this in a whole group setting and mix up the instructions however you like.
Let’s get started! Here are a few examples of how you can help young learners begin to access subitizing.
Step 1 Matching equivalent quantities—build the idea of conservation of numbers, same number different representation

Step 2 Comparing number and combining multiple sets to create sums

Step 3 Building relationships by linking Real World, Linguistic, Representational, and Symbolic using the above activities
Once students become familiar with subitizing, you can initiate lively discussions to use as springboards for other subitizing challenges and whole number sense routines. For example, display a dot arrangement, making sure numbers are appropriate, for 3–5 seconds then ask, “What did you see and how did you see it?” I used arrangements of eight.

Many of my students responded with eight, so It was very important for me to accurately represent what they saw to inform our discussions. Here are some examples:
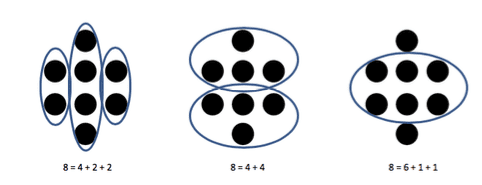
These kinds of activities are precursors to helping students have access to algebraic concepts. They help create a sense of equality, conservation of numbers, decomposing, and more. Being able to recognize equations as being balanced on both sides instead of just where the one correct answer goes is a huge development and deepens number relationships for students. After students have had some time to work with dot arrangements like this, let them have opportunities to explore true or false statements such as 4 + 2 + 2 = 6 + 1 + 1.
As students gain confidence in subitizing and their number sense, it is important to consider ways to differentiate for students based on their points of understanding. These could easily be created during centers or learning stations. Having Bingo daubers or pre-cut, one-inch squares will allow students to quickly create their own arrangements based on the numbers they need to practice. Some students can be at five while others are at nine, etc. Slide these into a sheet protector so students can easily exchange their arrangements to find the different ways they see to make the total number represented. If ready, their equations should match their drawn models. One caution, make sure students are actually subitizing. Circling ten individual dots to say 1+1+1+1+1+1+1+1+1+1=10 is not actually subitizing! Here is a sample launch: Use eight color tiles to make an arrangement. What numbers match your arrangement?
Student samples:

Note, the first student was able to accurately subitize and create equations based on what he/she saw. The second student shows great knowledge of working with ten and flexibility of thinking, but is no longer actually subitizing. It looks like this student is ready for a higher number!
Communication and productive discourse are essential to help students clarify information, deepen their reasoning, and move learning to long-term memory. Consider helping them learn with some sentence frames such as these:
- I agree with _____ because _______.
- I do not understand _________. Can you explain this again?
- I disagree with _______ because _______.
- How did you decide _______?
- I am thinking about this problem differently. Here is the way I solved it: _____________.
- My way is different from_____. Instead of____, I_____________.
- Can you explain the difference between ________and ________?
Interested in learning more about counting, subitizing, and other critical important foundations for math learning? You can explore Lisa’s presentation from the recent NCTM 2019 conference, Tool Time: It’s All About the Connections!, by visiting https://mathsolutions.com/contact-us/speaker-presentations/

 All Blog Posts
All Blog Posts
Comments