At-Home Learning | Kindergarten | Grades 1-2 | Grades 3-4 | Grades 5-6 | Grades 7-8 | HMH At-Home Learning Hub
Check back here daily for new resources!
Featured Problems:
Rich, interesting problems are powerful tools for student learning. The questions here are open-ended. There may be multiple answers or multiple approaches. Make time for your students to discuss and compare their solutions, either with you or with others. We hope these problems will spark students’ curiosity and lead them to investigate new questions.

Which of the following problems has the largest product? Try to figure it out by solving as few of the problems as possible.
3.2 x 17
24 x 2.9
50 x 3.5
2.4 x 29
1.7 x 50
5.0 x 36
Things to Consider:
Using mental math and estimation helps students spot unreasonable answers and find errors in their calculations. Encourage students to first think about what they know about these numbers and to use mental math to predict which problem will result in the largest product. For instance, a student could mentally estimate 24 x 2.9 by thinking of it as 25 x 3. If students seem overwhelmed, start with a smaller set of problems, such as 50 x 3.5, 1.7 x 50, and 5.0 x 36.
Using the digits 1 through 8, place one digit in each box.
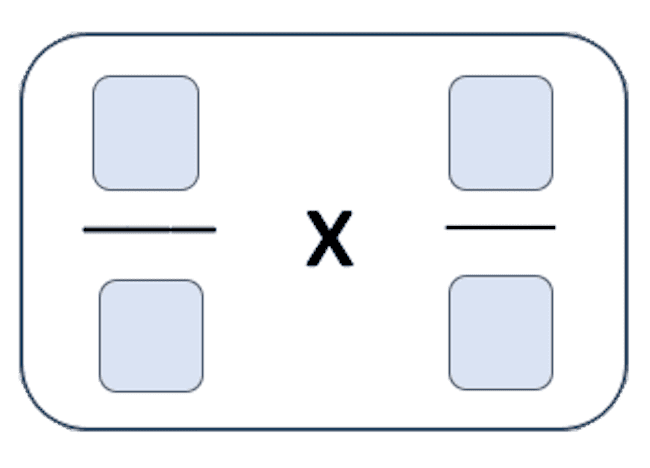
What is the least possible product? What is the greatest possible product? How did you make your number choices?
Things to Consider:
As students consider this problem, they use both their fractions sense – how fractions relate to each other – and their operation sense – what generalizations can be made about the product of two fractions that we’ve multiplied. Questions can encourage students to notice and generalize relationships. What do you notice about the larger fractions? How do you decide what numbers to use and where to put them?

Go on a scavenger hunt around your house. List five things you find that are examples of parallel lines and five things that are examples of perpendicular lines.
Things to Consider:
Problems like this one encourage students to use number sense as they estimate and make sense of the values of numbers. For instance, .00253 has a lot of digits, but it’s less than 1%. After a student explains his thinking about which expression represents the smallest number, it’s fine to use a calculator for the computation.

I am thinking of four odd numbers. They are divisible by five. The sums of the digits of each number create a consecutive number sequence. My first number is a square number. What are my four numbers?
Things to Consider:
This riddle is loaded with math vocabulary words. It may help students to first consider clues one at a time. What are some odd numbers? How do you know whether they are divisible by five? After students clarify their understanding of the clues, you might ask, “Which clue do you think is helpful to start with? Why?” After students have found a solution, encourage them to review each of the clues to test whether the solution fits the constraints of each clue. Encouraging students to evaluate the reasonableness of their own solutions encourages thinking and problem-solving. One possible solution to this riddle is 25, 35, 45, and 55.

There are five people in a family and their average age is 20. What might their ages be?
Things to Consider:
If children haven’t worked on open questions before, they may be unsure how to get started. You can provide them access into this problem, by encouraging them to start with an easier problem. What if two people had an average age of 20? What might their ages be? Why? Encourage children to try that strategy for the problem with five people?
Featured Videos:
Math in the Kitchen: A Recipe and a Half
What happens when you need to make a recipe and a half? We’re in the kitchen with Math Solutions Professional Learning Consultant Brandon Harms, turning dinner tacos into an exploration of proportions and ratios. What are you cooking tonight? Are you halving or doubling a recipe? Tell us on social media using #MathintheKitchen!
New Normal: Engaging in Error Analysis
Hollie Hartford gives tips for math teachers engaging in remote learning while keeping the 5 pillars of mathematics in mind. Try error analysis with your students!
New Normal: Tips for At-Home Math Learning
Math Solutions Professional Learning Consultant Brandon Harms shares 4 tips for at-home math learning to help you navigate this new normal.
Questions? Click Here to Contact Us


