Caterpillars

A Lesson for Kindergarten, First, and Second Grade

A Lesson with First Graders

by Leyani von Rotz and Marilyn Burns

Building, extending, and describing growth patterns is an important aspect of developing children’s algebraic thinking. In this lesson, children investigate caterpillars that grow, record on a T-chart, and then extend the pattern. The activity appears in Leyani von Rotz and Marilyn Burns’s new book, Lessons for Algebraic Thinking, Grades K–2 (Math Solutions Publications, 2002).

I gathered the students on the carpet in front of the board and drew on the board:

“How many circles did I draw to make my caterpillar?” I asked the students, then told them to whisper their answer to someone near them. I heard whispers of “Two” and “Three.”

“Let’s count the circles together,” I said, as I pointed to the head of the caterpillar. Together we counted to three.

“This caterpillar is one year old,” I said and wrote 1 year old next to the drawing.

“Watch as I draw a two-year-old caterpillar,” I said. Underneath the one-year-old caterpillar, I drew one circle with a face and antennas and then three circles for the body.

Next to the drawing I wrote 2 years old.

“What do you notice about my new caterpillar?” “He’s longer,” Ariel said.

“How many circles did I draw to make the two-year-old caterpillar?” I prompted. The students counted and responded, “Four.”

I then said, “The one-year-old-caterpillar has three circles and the two-year-old caterpillar has four circles. How many circles do I need to draw for a three-year-old caterpillar?” I wrote 3 years old on the board and a question mark where the drawing would go.

Most students responded, “Five.” I erased the question mark and drew a three-year-old caterpillar.

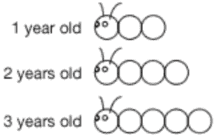
“So the one-year-old caterpillar has three circles, the two-year-old has four circles, and the three-year-old has five circles,” I said, emphasizing the pattern. “How many circles do you think a four-year-old caterpillar will have?”

“Six!” responded several students.

“I agree. How many circles would a five-year-old caterpillar have?” “Seven!” came the answer.

“How many circles will a ten-year-old caterpillar have? Think quietly and then talk with your neighbor.”

When they consider the number of circles for caterpillars in order, it’s easy for students to predict what comes next. They think about adding one more circle to the caterpillar that is one year younger. It’s more difficult for students to see the relationship between the number of years and the number of circles; that is, that the number of circles is two more than the number of years. I ask the question about the number of circles for a ten-year-old caterpillar to encourage children to think about this relationship, knowing that it’s beyond the grasp of many young children.

Some children guessed. Others figured out an answer by imagining the caterpillars, some correctly and others incorrectly.

I then said, “Let’s make a T-chart so we have a record just with numbers about how the caterpillar is growing. Then we’ll see how the T-chart can help us figure out how many circles the caterpillar will have as it grows older.” I drew a T-chart on the board.

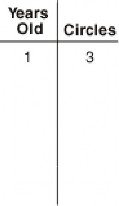
“Let’s say together how many circles the one-year-old caterpillar has,” I said. “Three,” responded most of the children.

On the T-chart I recorded a 1 and a 3, saying as I did so, “The one-year-old caterpillar has three circles.”

“How many circles does the two-year-old caterpillar have?” I asked. “Four,” came the response.

I wrote the numbers, saying as I did so, “So the two-year-old caterpillar has four circles.” I repeated the process for the three-year-old caterpillar.

“Now I need to write something down so I can remember what these numbers mean,” I said. I pointed to the top of the left column. “In this column, the one, two, and three stand for one year old, two years old, and three years old, so I’m going to write Years Old at the top. On the other side we wrote down three for three circles, four for four circles, and five for five circles, so I’m going to write Circles at the top.”

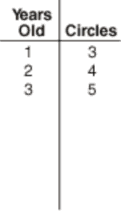
I labeled the columns of the T-chart.

“It’s in order!” Faraaz said. “One, two, three.”

“So what would come next in the left column?” I asked. “Four!” I wrote a 4 in the left column.

“And how many circles will a four-year-old caterpillar have?” I asked. “Six,” some students answered.

“Let’s see if the numbers on the other side go in order too,” I said, pointing to the right column. “Three, four, five, what would come next?”

“Six!” answered the class.

“Earlier we predicted that the four-year-old caterpillar would have six circles.” I wrote a 6 in the right column.

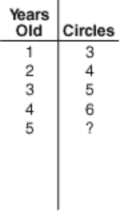
“In a moment you’re going to go back to your seats and think about what a five-year-old caterpillar would look like,” I said, writing the number 5 in the left column of the T-chart and a question mark in the right column.

I gave directions, “On your paper, draw a five-year-old caterpillar. Also, make a T-chart just like the one on the board, but write a number where I wrote a question mark. There’s one more thing to do, and that’s to figure out how many circles a ten-year-old caterpillar would have.”

As the students began working, I circulated among them, giving nudges and suggestions as needed. When children need help, I avoid breaking the task down into little steps; instead I try to keep the children focused on the investigation’s purpose.

Faraaz began by drawing a one-year-old caterpillar. He labeled it with the number 1 and then began his T-chart. He continued drawing caterpillars and adding information to his T-chart until he reached a ten-year-old caterpillar with twelve circles (Figure 1).

Veronica began by drawing a T-chart, labeling the columns, and filling in the first pair of numbers. She then drew a one-year-old caterpillar. She recorded the next pair of numbers and then drew a two-year-old caterpillar. Continuing in this way, Veronica reached the bottom of her paper after drawing a seven-year-old caterpillar. She turned her paper over and recorded up to a twelve-year-old caterpillar. When she was finished I suggested she label each of her caterpillars with its age.

Emanuel began by making a large T-chart that covered most of his paper. He filled it in as I had done, carefully referencing the board as he went. He then drew a picture of a five-year-old caterpillar and recorded a seven next to the question mark on his T-chart (Figure 2). This was a huge accomplishment for Emanuel.

A few minutes before the end of the period, I gathered the class back on the rug and said, “Raise your hand if you know how many circles the five-year-old caterpillar has.” All hands went up. “On the count of three, whisper your answer,” I instructed and counted to three.

“Seven!” they whispered. I recorded a 7 where the question mark had been and asked who would like to explain how he or she knew it had seven circles.

“’Cause the numbers go in order,” Jared said.

“So after seven circles, what’s going to come next?” I asked.

“Eight!” the class answered.

I said, “Let’s see if we can fill in our T-chart all the way to a ten-year-old caterpillar. A six-year- old caterpillar has eight circles. A seven-year-old caterpillar has nine circles.” I recorded these pairs of numbers and continued, encouraging the children to say the numbers along with me.

When I had recorded that a ten-year-old caterpillar had twelve circles, I said to the class, “I knew that was going to be right even without counting all the way down. I noticed another pattern.” I pointed to the first pair of numbers on the chart and said, “I know that to get from one to three, you can add two.” I pointed to the next pair of numbers and asked, “What do I add to two to get four?”

“Two,” the children answered.

I pointed to the next pair. “Three plus what gives five?” I asked.

“Two,” the children answered again. I continued in this way until the children had reported that six plus two gives eight. I then skipped down to information about the ten-year-old cater- pillar on the T-chart.

“We keep adding two to the years to get the number of circles,” I said. “I used that pattern for a ten-year-old caterpillar. Ten plus two is twelve, so I knew that the ten-year-old caterpillar had twelve circles.”

Together we continued and filled in the T-chart for an eleven- and a twelve-year-old caterpillar. “We have to stop now but I wonder if we could just keep going and going forever?” Several students nodded “yes” while others looked at me nervously as though they thought I might decide to cancel recess.

 

From Online Newsletter Issue Number 7, Fall 2002