Evens and Odds

A Lesson for Kindergarten, First, and Second Grade

by Stephanie Sheffield

Many first-grade children have learned to count by twos, at least up to ten. Some have learned the chant“ Two, four, six, eight, who do we appreciate.” And some know that when things are the same, we often say that they are “even.” However, most first graders have not thought about the relationship between these ideas and the properties of even numbers or about the difference between even and odd numbers. Stephanie Sheffield’s lesson helps develop the concept for children that a quantity is even if it can be divided into halves as well as helps them see the pattern that even numbers end with 0, 2, 4, 6, or 8, and odd numbers end with 1, 3, 5, 7, or 9. This lesson will be included in Stephanie’s forthcoming book, Teaching Arithmetic: Lessons for First Grade, to be published by Math Solutions Publications in fall 2001.

Every year our school PTA has a school-wide fundraiser. One year, in order to get the children excited about the event, we held an assembly to introduce the sale. The PTA moms provided a prize for each class that was wrapped like a present. If at least half of the students in a class sold at least one item, the class would get to open the box and claim the prize.

When we returned to the classroom after the assembly, I put the box on top of the file cabinet. I asked the class, “If half of the children in our class have to sell one item, how many children need to participate?”

Hands shot up in the air and numbers flew around, but it was clear that there was disagreement about how many students comprised half the class. I decided to use snap cubes to help the children work out the answer.

I pulled containers of cubes off the shelf and put one at each table. I said, “Each of you needs nineteen cubes. Who knows why you need nineteen cubes?”

Kristin answered, tentatively, “Because there are nineteen of us?” “What will each cube represent?” I asked.

“One kid,” Kristin responded.

I then gave the class directions. “Build a train with your nineteen cubes. Check with a friend to be sure your trains are the same size.” I waited until all of the children had done this.

I then said, “Now, break your train in half.” When the children snapped their trains into two pieces, some thought that they had two equal trains. Their new trains appeared to be the same, and they didn’t think to check by standing them up or laying them flat on the desk. Alex, however, held up his two pieces.

“I don’t think this is right. They don’t match,” he said.

“Yeah, they’re supposed to be the same,” Andrea agreed, comparing her two trains. “What do you mean by that?” I asked.

“It’s like an apple,” Richard explained. “If you cut it in half, you and your friend each get a part. But it has to be fair.”

“So if you cut something in half, how many parts do you get?” I asked. “Two!” they all said together.

“And what can you tell me about the two parts?” I continued. “They are always the same,” Mukund replied.

“Equal,” Christian added.

“The question is, how many students are there in half our class?” I said. “How can the cubes help you find out?”

Kevin answered, “It’s either eight or nine. One of the trains has eight and one has nine.” Kevin had miscounted the cubes, but he was aware that the trains were one cube apart.

I said, “But if we break our train into halves, each has to be the same length. How can you divide a train with nineteen cubes into halves?” Students tried over and over, snapping the cubes together and then separating them. Each time the result was unequal trains.

Finally, Chloe said, “I just don’t think this is going to work. One train is always one cube taller.”

“It would work if we threw out one cube,” Christian suggested.

“It won’t work!” Kierra cried in exasperation. “One of the trains is always bigger than the other one.”

Since some of the students were becoming frustrated, I stopped their investigation for a few minutes of discussion. I said, “The reason this is difficult is that we can’t cut a cube in half and put part of it on one train and part on the other train. But using cubes is still a good model for solving our problem about how many children make half the class because we can’t divide a student up, either. For this problem, the best we can do is to say that half of our class is either nine or ten.”

“Let’s use nine!” Andrea exclaimed. “That way we’ll have a better chance of getting to open the box!”

I then extended the question to have students use cubes to investigate dividing other whole numbers in half. I said, “Kierra said that nineteen doesn’t work. Who knows what she means by that?”

Lauren said, “She means you can’t split it into two even trains.”

“Do you know a number of cubes that a train could have so it does work to split it into halves?” I asked.

Chloe raised her hand. “If we got rid of a cube, we’d have eighteen, and that works,” she said. The children verified with the cubes that this was so. I went to the board and drew a vertical line to make two columns. I titled the left-hand column “Works” and the other column “Doesn’t Work.” I recorded 19 under “Doesn’t Work” and 18 under “Works.”

I got the children’s attention and gave directions for further exploration. “You’ll each choose a number between ten and twenty.” Immediately, hands dove into the containers of cubes. I took a minute to call them back to attention and I waited until all hands were off the cubes.

Then I continued, “After you count out the cubes, make a train and try to break it in half. Be ready to report to the class the number you chose and if it belongs in the ‘Works’ or ‘Doesn’t Work’ column.”

The children went to work. Some unsnapped the cubes in their trains and then began over again to count out cubes. Some started with the train of nineteen and took some cubes away.

When I saw that all of the children had explored at least one number, I called for their attention. I called on several children to report on the numbers they had investigated, recording each number on the board in the correct column to indicate whether it could or couldn’t be broken into two equal parts.

After I had recorded six numbers, I focused the class on the labels of the columns. I asked, “Who can explain what we mean by ‘Works’ and ‘Doesn’t Work’”?

I waited until most of the children raised their hands and then called on Mukund. “All the numbers that work, you can make two trains that are the same with them,” he said.

Next I called on Tatyana. “Those numbers,” she said, indicating the “Doesn’t Work” column, “all have a leftover cube when you try to break it into half, but the other ones work without a leftover.”

I continued asking children to report numbers until I had recorded all of the numbers from 10 to 20. Sometimes children reported a number that I had already recorded. In these cases, we used the information as a check.

I then asked the class to consider numbers less than ten, this time first making a prediction about whether or not the number would work, and then building the train and snapping it in two. To begin, I asked the class, “Do you think six will work or not?”

Richard responded, “I think it will because I know that three and three is six.” Some children agreed and others weren’t sure.

I said, “When you make a prediction as Richard did, you can then test your prediction with the cubes. You’d build a train with six cubes and see if you can break it into halves.”

I stopped the children from doing this immediately and gave the class one more direction. I said, “See what you can find out about numbers smaller than ten. Each time, make a prediction first, and then test your idea with the cubes.” The children got busy again.

“All the doubles work!” Andrea exclaimed after a few minutes. “Three and three is six, and four and four is eight, and five and five is ten!”

 

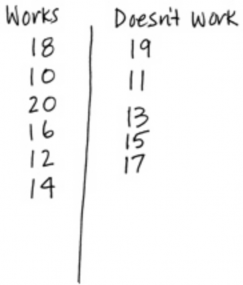
Lauren stopped her building and looked at the chart. Then she looked at Andrea and said, “All the numbers on the ‘Works’ side are doubles. See, there’s eight and eight is sixteen, and six and six is twelve.”

After a few more minutes, I called the class back to attention again. I had students report the numbers they had investigated and I recorded them in the correct columns. I did a quick check to be sure that I had recorded all of the numbers.

I then said, “There’s another label we could give to each of these columns.” On the board I wrote Even Numbers above “Works” and Odd Numbers above “Doesn’t Work.”

“Do we have an even number of students in our class or an odd number?” I asked.

“An odd number!” was the resounding response.

“Can someone explain what you think even numbers are?” I asked.

Jesse volunteered: “All the even numbers, you can make a train with them and then make two even trains, but the odd ones don’t work.” Heads nodded and children murmured their assent.

I now posed a related question. “What if we had nineteen cookies? Could we split them into two equal parts? Talk to your neighbor about what you think.”

After a few minutes I asked for discussion. Kierra raised her hand. “Cookies are different,” she said. “You can cut cookies in half, but you can’t cut cubes.”

Reordering and Recording

I asked each student to take out a piece of paper and a pencil, draw a line, and label the left- hand column Even Numbers and the right-hand column Odd Numbers. I did this on the board and waited until they had all done so on their papers. One reason I wanted them to have the experience of recording the numbers themselves is that sometimes when they do the writing themselves, they notice patterns they missed when looking at the board. Also, this serves as a model for organizing lists of numbers and gives them a model for forming the numerals correctly. And lastly, if they have this record to take home, it may spark a conversation with their parents about the math they did in school today. Having the papers in their hands provides a starting point for this discussion and helps them remember the mathematics involved.

“You’ll each write down the numbers from each column, but we’ll put the numbers in order from least to greatest. Let’s do it together. What’s the smallest number you see on the board in the ‘Even Numbers’ column?” They all responded, “Two,” and I wrote it at the top of the new column I had labeled. The next larger number they found was four, then six, then eight. By now, many of the children noticed the pattern of counting by twos and they reported quickly, without searching. But since many of them were less confident counting by twos beyond ten or twelve, they slowed down a bit at that point. We ordered the numbers in the “Odd” column in the same way.

When we had ordered all of the numbers, I asked, “What patterns do you notice when you write the numbers this way?”

Richard raised his hand. “The even numbers go two, four, six, eight, then the numbers on the right side go zero, two, four, six, eight.”

“And the odd numbers go one, three, five, seven, nine,” Angelo said.

The underlying mathematics of even and odd numbers and their relation to doubles and halves is important to a first grader’s growing number sense. While this investigation arose from a situation that occurred naturally in our classroom, the opportunity doesn’t always come up. Still, I can provide the children the same opportunity by structuring the lesson around a different situation that calls for figuring out how many children are in half the class. For example, if we divide the class into two teams, can we have the same number of children on each team? Or, if half of our class gets photos taken before lunch and half after lunch, how many will be in each group? Whatever the problem, I always use the cubes so that children have the chance to verify their thinking with physical objects.

 

From Online Newsletter Issue Number 1, Summer 2001