More than One
 All Classroom Lessons
All Classroom Lessons

A Lesson for First and Second Graders
By Jamee Petersen
Miriam Schlein’s More than One (New York: Greenwillow, 1996) introduces the concept that one unit can be made up of more than one thing. One pair is always two, one week is seven days, but one family can be two, three, or more people.
Here, first and second graders use mathematical language to describe their self-portraits, applying the concept that one can be an exact number or can describe a variable number of things. This lesson appears in the new book Math and Nonfiction, Grades K–2, by Jamee Petersen (Sausalito, CA: Math Solutions Publications, 2004).
I gathered the students on the rug to read More than One aloud to them. When I finished reading, I asked, “What did you learn about the number one from this book?”
“One can mean one like one sun in the sky, but sometimes it means more than one,” Brock offered.
“One can mean a really big number like a billion or trillion,” Amanda stressed, “like sand. One beach has so much sand we can’t even count it all, but all the sand put together is just one beach.”
“One can mean nine. Like in baseball, nine players make a team. But one team can also mean five, like a basketball team, and a football team has eleven players on the field at once,“ explained Mark.
“So, one can refer to one exact thing, but one can also refer to groups that have more than just one in them,” I said. On the board I wrote More than one and under it I created a two-column chart, titling the columns exact numbers and variable numbers. Although variable wasn’t a term that the students were familiar with, I introduced it by simply using it throughout the lesson along with more familiar language like the word changeable.
“What were some of the ideas presented in the book about the number one that we could list in our exact numbers column?” I asked.
Meagan said, “Pair would go there.”
“You’re right,” I confirmed. I recorded the word pair under the heading exact numbers and asked, “Can you explain why, Meagan?”
“Well, like a pair of shoes is two, but it’s one pair of shoes,” she said.
“One dozen always means twelve, like a dozen doughnuts,” said Jasmine. I added dozen to the first column in the list.
“One week is always seven days, so week should go under exact numbers,” Sari directed. I wrote week in the first column.
“I think team would go there even though it changes because it’s still an exact number,” Eric said. I understood what Eric was trying to explain and saw that a few other classmates shared his reasoning. I asked Sammy to explain further.
“It’s like one team is an exact number, like nine players on a baseball team,” she shared. “But if you’re talking about another team, like a volleyball team, then the number would be six, so one team is six players.”
“I think team would go on the various side because it is like family; it depends on what kind,” Julian said. I didn’t correct Julian’s mispronouncing variable. Various is a word that Julian was familiar with, and I felt confident that he would make the shift after hearing variable used more often.
Others agreed with Julian, so I wrote team under both the exact numbers and variable numbers columns.
“How was the number one used in the book to describe groups with changing numbers?” I asked and recorded as the children reported. Soon our list looked like this: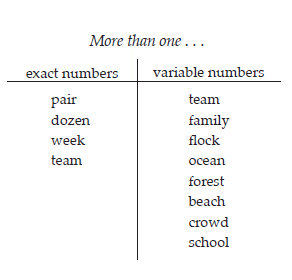
Then I introduced the activity and said, “So the book More than One showed us how one can mean more than one. For example, we are one class, but within this class are twenty-six students. I’d like you to begin thinking about the one you that helps make up our one class. Today we are going to create self-portraits and describe them using some of the mathematical ideas presented in the book. For example, let’s focus on our faces.”
I asked the students to turn so they were knee-to-knee with the person sitting next to them. “Study your partner’s face. How many eyes do they have?”
“Two,” chorused the class.
“How many pairs of eyes do they have?” I emphasized by pointing to pair on our chart. “One,” the students replied.
I continued inquiring, asking about the number of ears and number of pairs of ears, and then about noses and nostrils, mouths and lips.
I moved on to include the variable numbers. “So we have many pairs on our face—a pair of eyes, ears, nostrils, and lips. Now everyone smile a big toothy smile at your partner. How many smiles do you each have?”
“One,” the students replied, giggling.
“How many teeth are in that smile? I want you each to count your own teeth using your tongue and then open up and have your partner check your count just like a dentist might look into your mouth.” The students were a little silly during this activity but it was worth-while because it generated a set of numbers that varied because some of their smiles were missing teeth.
Giovanna said, “I have a smile with nineteen and a half teeth because I lost this one and now I have a big tooth coming in, but it is only halfway in. So I have nineteen teeth plus this half tooth.”
“So we each have one mouth or smile with one set of teeth, but the number of teeth that makes up that smile or set can be different. Some of you have twenty-four teeth, some have twenty-five and a half, and others have twenty-six. The number of teeth varies,” I said, pointing to
the heading variable numbers on the board, “but the number of mouths on each face is still just one.”
We talked about the tops of our heads and the hairs on them being too many to count, like the trees in the forest and the birds in the flock we had seen in the book’s illustrations.
I asked the students to turn and face me. I told them again that they were going to be drawing portraits of themselves. “Then you’ll write at least five mathematical statements that describe your face,” I said. For those students who needed an extra mathematical challenge or who enjoyed drawing, I suggested, “Or you can draw your entire body and include additional facts about one part. For example, you have one hand but five fingers.”
I made mirrors available to students—a full-length mirror and several hand mirrors. Some students studied themselves carefully with the mirrors before they got started and as they drew. Others drew their portraits without so much as a glance in a mirror.
A sentence starter is always helpful for some students. I listed some prompts on the board for them to record on their papers and think about:
I have two_______ but just one_______ .
I have_______ five but just one_______ .
I have lots of_______ but just one_______ .
The idea of “more than one” is depicted in Figures 1 and 2. Joe’s and Morgan’s drawings both show eyelashes. Each chose to handle this number differently. Joe used an exact number, 4, and then was sure that his drawing matched that number. Morgan was comfortable using an approximation, stating that she had lots of eay lashes, a statement that accurately describes her drawing.

Figure 1. Joe worked diligently to complete his illustration. The
concept of “more than one” came easily to him, but expressing
it in writing proved more challenging.
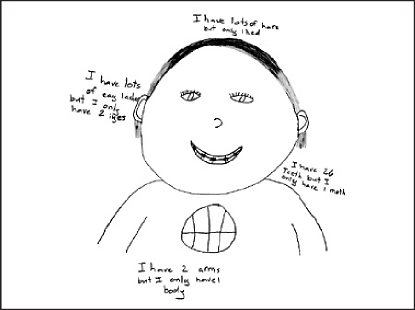
Figure 2. Morgan’s labels surrounded her self-portrait.
After the students had completed their self-portraits, I collected the pictures and hung them in the hallway. Next to them I posted a sheet of paper on which I had recorded two questions taken from the book, leaving space beneath each question to record answers.
Can one be more than one?
Can one be different, different every time?
The following day I asked the students to talk about their drawings and what they wrote. I asked them to answer the first question I had written: “Can one be more than one?”
“Yes,” they replied together. I wrote Yes.
I read the next question: “Can one be different, different every time?” Again the students replied easily: “Yes.”
I wrote: Yes, one can be twenty-six kids in a class. How many are in your class? I hoped this last question would prompt readers of our display to think about the mathematical idea being presented. Over the next week, many classes stopped outside of our room to answer the questions and take note of the mathematical concepts the students had illustrated in their drawings.
From Online Newsletter Issue Number 16, Winter 2004–2005

Comments