One Riddle, One Answer

A Lesson for Fifth Graders

“Who can explain what a riddle is?” Danielle Gilligan asked her fifth graders.

“It’s like a mystery you have to figure out,” Jill said.

“It has clues that help you solve it,” Ramon added.

“I have a book about a riddle,” Danielle said. “I’m going to read the story and stop at a certain point so that you can try to figure out the answer to the riddle.”

Danielle started reading One Riddle, One Answer aloud. Her students learned about Aziza, the sultan’s daughter, and how the sultan’s advisors all wanted their sons to get a chance to become Aziza’s husband. Danielle stopped reading at the part where Aziza proposes that she write a number riddle. The princess tells her father that she would prefer to marry the person clever enough to answer her riddle. The sultan agrees.

“I’m going to show you the riddle that Aziza wrote,” Danielle said. “I’ve written it on a piece of chart paper. We’ll read the riddle together, then I want you to think about the clues silently first. You can use scratch paper to jot down your thoughts. Then, whisper your ideas about the answer to a partner.”

Danielle posted the chart paper on which she’d written Aziza’s riddle:

• Placed above, it makes greater things small.
• Placed beside, it makes small things greater.
• In matters that count, it always comes first.
• Where others increase, it keeps all things the same.
• What is it?

Danielle first gave students time to think and take notes. Then, as the students shared their ideas with their partners, she circulated, listening to their guesses. Some thought the answer was one; a few thought that it was zero; many were completely stumped.

Danielle then continued reading until she came to the part in the story where the scholar guesses that the sun is the answer to Aziza’s riddle. She stopped at this point and addressed the class.

“The scholar’s guess is true for the first line in the riddle (‘Placed above, it makes greater things small’),” she said, “but does that answer work for each of the other clues?”

“No,” Anna responded. “It doesn’t make sense for the others. The sun doesn’t come first when you count.”

“That’s right,” Danielle confirmed. “An answer to a riddle must fit all the clues, not just some of them.”

Danielle continued to read. Each time a suitor in the story guessed an answer to Aziza’s riddle, Danielle stopped and checked with the students to see if the answer fit all the clues. When Ahmed, the farmer in the story, guessed that the answer to the riddle was the number one, Danielle again checked with the students to see if it worked with all the clues, and it did.

“But zero works too!” Amanda cried.

Danielle was taken aback. She later confided that she hadn’t thought about another possible answer. “Explain what you mean,” she said.

“Well, placed above a number, it works,” Amanda explained. “Like, if you put zero above five when you multiply, it makes five smaller. And it works for any number you multiply it by.”

“You mean like this?” Danielle asked, recording Amanda’s idea on the board:

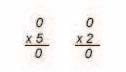
Amanda nodded and continued with her argument. “Placed beside other numbers, it makes them greater, just like in Aziza’s riddle.”

“Come up and show us,” Danielle urged. Amanda walked up to the board and wrote:

10      20      50

“When you put zero beside these numbers, it makes them bigger,” she said. “Zero next to one makes it ten; zero next to two makes it twenty. And when you count, zero comes before one on the number line!” she exclaimed.

“And on the thermometer, zero comes before the number one,” Joe added.

Elise piped in, “And for the last clue, zero keeps all things the same when you add zero to it, like zero plus one is one or zero plus ten is ten.”

“I’m impressed with your reasoning. I hadn’t thought about zero as an answer,” Danielle exclaimed.

“I disagree,” Kyle challenged. “When you count, you don’t start with zero, you start with one.”

“But if you’re counting down the days till Christmas, on Christmas there’s zero days left!” Amanda countered.

Danielle didn’t interfere. Getting students to argue passionately about their ideas in math class is often difficult to achieve. Giving students interesting problems to solve, like Aziza’s riddle, can motivate them to develop and exchange ideas.

When the short debate was over, Danielle acknowledged that there could be more than one correct answer to the riddle. Then she finished reading the story, including a section at the back of the book where the author explains how the number one works for each clue.

“Aziza’s riddle helped us think about number riddles,” Danielle said. “Let’s try to write a number riddle together. First, you have to think of a number to write about. Then you have to write some clues. I want you to practice by brainstorming some possible clues for the number ten.”

Danielle gave the students about five minutes to work in groups. She then called the class together and wrote some of the clues the students came up with on the board:

• Count your fingers on both of your hands.
• If you cut me in half and multiply me by 7, you get 35.
• If you multiply a number by the mystery number, you’ll always end in zero.
• The age of a fourth-grader.

Then Danielle gave feedback on the clues. “When you write a riddle, the first thing you do is brainstorm a list of possible clues, just like we did for the number ten,” she said. “It’s OK if answering one of the clues gives away the secret number, but try to be tricky with your clues, like Aziza was with her riddle.”

When the class was finished brainstorming clues for the number ten, Danielle gave the homework assignment of writing one riddle sentence for the number one-half. She explained, “Use pictures, words, and numbers to explain why the answer to your riddle sentence is one-half.”

The next day, Danielle asked for volunteers to share their riddles. Some students revealed some very sophisticated thinking about one-half, while others exposed misconceptions.

Keaton shared first, “If you have a glass of water, the water hits the middle,” he read, showing a picture he drew of a glass half-filled with water.

Then Nicholas read, “This number is between zero and one and if you multiply this number by two you get one.” On the back of his paper, he explained why 1/2 x 2 = 1: If you multiply it by 2 you get 1 because 1/2 + 1/2 = 1. (See Figure 1.)

Here are some other clues that students wrote and shared:

• I am half of 7, subtract 3.
• The fraction you’re guessing is greater than 1/4 and less than 1.
• If you double 1/4, you get this number.

Danielle then said, “Now that you’ve had some experience with writing clues for the numbers ten and one-half, you’re going to each choose a number, brainstorm clues for that number, and then write a riddle.”

“How many clues does the riddle have to have?” Lisette asked.

“Aziza’s had four clues, so try to write a riddle with at least four,” Danielle responded.

Soon, the class began to hum with conversations as students shared their ideas with one another. As Danielle circulated, she encouraged students to think of subtle rather than obvious clues. After about thirty minutes, she pulled the class back together.

“Let’s have some volunteers read their riddles. After they read their clues, we’ll try to guess the answer.”

The following are a couple of riddles that students shared (see Figures 2 and 3).

---

Related Publication:
Math and Literature, Grades 4–6, Second Edition
by Rusty Bresser