Ten-Frames Lesson: Race to 20
 All Classroom Lessons
All Classroom Lessons

Overview
In this game, students roll a die and place that number of counters on a double ten-frame in an effort to reach 20 first. This game builds students’ understanding of landmark numbers, specifically ten and twenty. Through the use of two colors of counters, students decompose the number twenty and use number strings to compose twenty. The game also naturally lends itself to encouraging students to compare numbers. Further ideas for introducing and summarizing the game are included in the “Teacher Reflection” section. In the assessment, students use their experience with Race to 20 to compare quantities and connect the game to number sentences.
Time
20 minutes
Materials
dice, 1 per pair of students
double ten-frame (Reproducible D), 1 per student
counters, 25 each of two colors per student
Extension
dice with a small sticker on one face, 1 per pair of students
double ten-frame (Reproducible D), 1 per student
counters, 25 each of two colors per student
Related Lessons
You might teach the following lessons first:
◗ R-4 Number Strings
◗ R-5 Adding Nine
◗ R-6 Sums One More Than Ten
Consider these lessons as a follow-up:
◗ P-1 Two-Color Counters
◗ P-3 Mystery Sums
(Beveled box)**
Key Questions
◗ How many more counters do you need to have ten?
◗ How many more counters do you need to have twenty?
◗ How many more counters do you have compared with your partner?
◗ How would you add the counters you have so far?
**
Teaching Directions
-
Explain to students that they will be playing a game using one die and two double ten-frames. The double ten-frame is their game board; each student will have one.
-
Ask a student volunteer to help you model the game for the class. Ask her to roll the die and call out the number rolled. Then ask her to place that number of counters on her double ten-frame. Emphasize that the counters must all be of the same color.
-
Thank the volunteer student and ask her to pass the die back to you. Roll the die and call out the number rolled. Place that number of counters on your game board. Make sure you are using the same color of counters as the volunteer student did; point this out to students.
-
During the second turn, repeat the process but use the other color of counters. Ask the class, “How many more does each of us need to fill in one ten-frame or one double ten-frame?”You might also ask,“How many more do I need to have ten [or twenty] counters? How many more does my partner need to have ten [or twenty] counters?”
-
Explain to students that when a player reaches 20 (that is, fills his or her double ten-frame), he or she has won the game. Note that players do not have to roll an exact amount to win. Let students know they can place any extra counters under their game board.
-
Continue playing the game until someone wins. Once a winner has been declared, explain that students then need to record number sentences that represent their sequence of rolls. Ask students to tell you the number sentence that represents the winner’s rolls and record their ideas on the board. Then ask students for strategies to add the number string. Repeat the same for the double ten-frame that didn’t reach 20.
-
Make sure to ask students if they have any questions before turning the game over to them.
-
Pass out two double ten-frames, one die, and fifty counters (twenty-five each of two colors) to each pair of students.
-
As students play the game, circulate and ask questions (refer to the key questions).
-
Summarize by choosing a focus such as the following:
- address how to figure out how many more or less you have than your partner
- work on strategies for adding number strings
(beveled box)**
Teaching Tip:Passing the Dice
By asking students to pass the dice, you are modeling the appropriate behavior expected of them during the game. In addition, having students pass the dice in a friendly manner instead of grabbing the dice will ensure fewer disagreements.
**
(beveled box)**
Teaching Tip:Emphasizing Counter Colors
Make sure students understand why, on each turn, it’s important to alternate between the two colors of counters. This way, they can easily see each roll depicted on their double ten-frames.
**
Time Saver
As students are settling in for the day, ask the first two students who arrive to help with preparing the day’s math materials. These students can count out groups of twenty-five same-color counters and place each group in a plastic sandwich bag. This makes it easy to distribute the counters when it comes time to do so. Alternatively, have each student count out a group of twenty-five counters in each of two colors as soon as they enter the room. Once again, they can place the counters in plastic sandwich bags so you can easily distribute the materials when the time comes to do so.
(beveled box)**
Teaching Tip:
Race to 20 calls for each pair of students to have fifty counters. If you do not have enough of one kind of manipulative to accomplish this, consider letting students play pairs against pairs. Alternatively, break up manipulatives among the pairs—give color tiles to a few groups, Snap Cubes to other groups, and two-color counters to other groups.
**
Game Directions: Race to 20
Objective
Players roll a die and use counters to build that number on their double ten-frames. The player who reaches or goes over 20 first is the winner.
Materials
2 double ten-frames, 25 counters each of two colors, and 1 die for each pair of players
Directions
-
Player A rolls the die and uses one color of counters to build the number on his or her double ten-frame. Player A passes the die to Player B.
-
Player B rolls the die and uses the same col- or of counters to build the number on his or her double ten-frame. Player B passes the die to Player A.
-
Player A rolls the die and uses a different color of counters to build the number on his or her double ten-frame. Player A passes the die to Player B.
-
Player B rolls the die and uses the same color of counters Player A just used to build the number on his or her double ten-frame.
-
Play continues until one player reaches or goes over 20. If a player goes over 20, place any additional counters below the game board.
-
Each player records the number sentence that matches his or her rolls for the game on a sheet of paper or in a math journal. For example, if Player A rolls 5, 3, 2, 6, 3, and 1, he should then record 5 + 3 + 2 + 6 + 3 + 1.
-
Players add their number strings to verify they match the number of counters on their double ten-frames.
Note: For each roll, players alternate the color of counters used to build the number on their double ten-frames so they can easily see a record of their rolls at the end of the game.
Homework
For homework, you can send materials and game directions home with a note attached asking the parent and child to play the game three times.
Extend Their Learning!
Place a small sticker, such as a smiley face, on one face of each die being used (typically the face showing 1). Explain to students that when they roll the die and get the stickered face, they must choose a key question to answer. Display the key questions where all students can see them. Decide if that roll will be their turn or if they can roll again.
Key Questions
◗ How many more counters do you need to have ten?
◗ How many more counters do you need to have twenty?
◗ How many more counters do you have compared with your partner?
◗ How would you add the counters you have so far?
Assessment: Race to 20
After students have been playing the game for a while, consider assessing them using the Race to 20 assessment (Reproducible 17), which can be ad- ministered in small groups or to the whole class. Each student will need his or her own Race to 20 assessment and access to counters or hundreds charts (Reproducible J).
The first question shows a game board with all the squares shaded in, some gray and some black. Tell the students this was a winning game board from a round of Race to 20 and that gray and black indicate the rolls and the two colors of counters used. Ask students to write a number sentence that matches the game and show how they would add the number string together.
The second question shows two game boards, each partially filled in. Tell students this is a Race to 20 game that is still being played and you want them to figure out who is ahead and by how much. They can use counters or the hundreds chart at their seats, but they need to show their thinking on their paper.
Teacher Reflection
My Race to 20 Experiences
Introducing the Game
I introduced Race to 20 by showing a class of second graders a double ten-frame and explaining that this would be the game board. I used Snap Cubes for counters.
“How can you figure out how many spaces there are on the double ten- frame game board?” I asked the class.
“I see twenty squares because two ten-frames is ten plus ten,” Alex said. I wrote 10 + 10 = 20 on the easel.
“I counted by fives,” Viviane said. Then she pointed to the end of each row on the double ten-frame and added, “Five, ten, fifteen, twenty.”
I recorded her skip-counting on the easel and called on Timothy. “I saw two ten boards and knew that was twenty.”
“Mathematicians would record that as ‘two groups of ten equals twenty,’” I explained as I recorded 2 × 10 = 20. Even though I had not formally taught multiplication, I wanted to give students experiences with multiplication when it connected to their thinking.
I then told the students that the objective of the game was to fill up their double ten-frame before their partner filled his or hers. Each player would roll the die and place that number of Snap Cubes on the game board. I emphasized that they would use two colors of Snap Cubes so that they would be able to see the individual rolls. I called on Lucy to play the game with me and handed her a double ten-frame while simultaneously placing one in front of me.
Lucy rolled a 4 and placed four red Snap Cubes on her board. I reminded the class that it was important that the person whose turn it was handed the die to her partner when she was finished. I wanted students to learn not to grab the die before their partner was finished with his or her turn.
Lucy handed me the die and I rolled a 3. I placed three red Snap Cubes on my game board.
“How many more Snap Cubes do I need to fill up one ten-frame? How do you know?” I asked.
“You need seven. See—the bottom row has five empty and then there’s two empty spaces at the top. Five and two is seven,” Maria explained.
“How many more cubes does Lucy need fill up one ten-frame?” I continued the questioning.
“She needs six more. I can see five empty and one left over on the top row,” Marcus explained.
Lucy picked up the die and rolled a 5. This time I instructed her to use the yellow Snap Cubes. I then rolled a 2 and placed two yellow cubes on my game board.
“Who’s winning?” I asked. “Lucy!” the class said in unison.
“How many more cubes does Lucy have on her game board compared with my game board?”
“I think she has four more cubes than you do,” Marcus declared. “How did you think about that, Marcus?”
“Lucy has the top row filled up and so do you. You need four cubes on the bottom row to be the same as her.”
“Do you agree or disagree with Marcus’s answer, and can you explain?” I asked the class.
“I agree! I think if you put them together, then her line will have more.
I think there would be four left over,” Leah explained.
I took the cubes from my game board and snapped them together to create a tower and asked Lucy to do the same. We then compared our towers by holding them next to each other. Lucy counted the leftover Snap Cubes from her tower that didn’t partner with any of my cubes.
We continued the game and I occasionally stopped the play to ask “How many more?” questions. Eventually our game boards looked like this, and it was Lucy’s turn to roll:
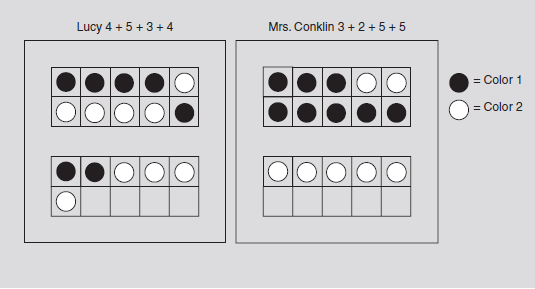
“Lucy needs only four Snap Cubes to win, but she rolled a five. How many cubes will Lucy have left over when she fills the game board?” I asked the class.I explained to the group that Lucy could win if she rolled a 4, 5, or 6. I told them it was not necessary to roll exactly what was left on the game board. Lucy rolled a 5 and I instructed her to place five Snap Cubes near her game board.
“I think she’ll have one left over. I put up my five fingers, put four down, and had one left up,” Edgar said, demonstrating.
“I counted up from four and said, ‘Five,’ so she’ll have one left over,” Jamel said.
I asked Lucy to fill up her game board and check to see what was left over. She filled up the four empty spaces and held up one leftover cube. She placed it below the game board. I congratulated Lucy on getting to 20 before me and focused my attention on her game board.
“Looking at Lucy’s game board, I think I can tell the story of her game. I can see what numbers she rolled each time by the color of the Snap Cubes. Is someone willing to try to tell the story of Lucy’s Race to Twenty game?” I paused to give students time to think. I called on Javon first.
“She rolled a four, then a five, then a three, then a four, and another four,” Javon said. I wrote 4 + 5 + 3 + 4 + 4 for everyone to see.
“Do you agree or disagree with Javon’s idea and can you prove your thinking to us?” I prompted the class.
“I remember her rolling a five at the end of the game, but her game board shows four,” Edgar said, scratching his head. “Do we say five or four in our story?”
“Interesting question. I agree Lucy rolled a five, but she could use only four Snap Cubes to fill the game board. Let me revise what I said earlier. Let’s tell the story of Lucy’s game board. We know that the last roll some- times won’t match what we put on the game board, so it will be the story of how her game board looks.” I watched as the class nodded in agreement. “Who can prove Javon’s idea of Lucy’s story?”
“We can see four red cubes,” Maribell moved the first four cubes from Lucy’s game board to the side. “Then she has five yellow ones, and three red ones. Here are four yellow ones and four more red ones. Javon’s number matches!”
“So, we have the story of how Lucy raced to twenty. Let’s check the numbers one more time. Look at the number string I wrote when Javon explained Lucy’s story. What numbers do you see that you can add?” I asked. The class had been working on addition strategies and number strings for a couple of weeks.
“I see some fours and I know how to skip-count by fours. So four, eight, twelve is what I did first,” Marcus explained. I wrote 4, 8, 12 on the easel, then asked him what he would do next.
“Three more makes fifteen. Oh easy—fifteen and five is twenty,” Marcus exclaimed, proud of himself for making his last combination “easy.” I re- corded 12 + 3 = 15 and then 15 + 5 = 20.
“Thank you, Marcus. Who has another way?”
“Well I started at the end; four and four is eight, and five and three is eight, so now I have a double. Eight and eight is sixteen. Sixteen and four makes twenty,” Maribell explained. I recorded 4 + 4 = 8, 5 + 3 = 8, 8 + 8 = 16, and 16 + 4 = 20.
“So Marcus skip-counted to help him. Maribell looked for doubles. Did anyone add the numbers another way?”
“I looked at her game board to help me,” Vincent shyly contributed. I assured him that his insights were helpful and we would like to hear more about his thinking.
“Four and five is nine, and four and four is eight. I took the three and split it into a one and two, just like on her board. Nine and one is ten, and eight and two is ten, so it all equals twenty.” Vincent showed the 3 on the board, split between the first and second ten-frames as 1 and 2. I was pleased that Vincent was decomposing numbers and using the game board to help him make sense of that concept. I recorded 4 + 5 = 9 and 4 + 4 = 8. Then I wrote 3 = 1 + 2 and continued by adding 9 + 1 = 10 and 8 + 2 = 10. We continued by telling the story of my game board, recording number sentences, and checking to make sure those number sentences added up to fifteen.
“So today during your exploration, you will play Race to Twenty with a partner. When one player fills up his or her double ten-frame, the game is over and you will record the story of your game board with number sentences. Then I would like you to add up the numbers to make sure they equal the number of counters on your game board.”
Exploring the Game
As students got started playing the game, I observed several groups before be- ginning my questioning. I have found that when I observe without interacting with the groups, I can formatively assess what they know and don’t yet know. I use this information to guide my future lessons or daily routines. For example, I overheard Edgar and Leo talking about their game. They were discussing who was ahead. I heard Leo tell Edgar he was ahead of Edgar.
Edgar responded, “Yeah, but not by much.”
Leo replied that he didn’t know by how much, but he knew he had more. I made a note to return to the idea of how many more during the summarization of the game.
Summarizing the Game
“I noticed when some of you were playing, you would say things like ‘I’m winning!’ or ‘I’m losing right now.’ How did you know if you were winning or if you were losing?” I asked the class. I wanted to use the students’ common language as a context for introducing mathematical concepts.
“When I look at our game boards, I can tell who has more because they have more filled in,” explained Gabby.
I decided to fill in two game boards as an example and ask Gabby to tell us which game board was winning.
“The one with fourteen. The other one has eleven, and that is smaller than fourteen.”
“Do you agree or disagree with Gabby’s idea?”
“Yeah, I agree. Fourteen is greater than eleven,” Leo said, nodding. “Who can restate what Leo said in your own words?”
“Leo is saying fourteen is bigger than eleven,” Javon restated.
“What I am wondering is how much bigger fourteen is than eleven. Another way mathematicians might say that is ‘How much greater is fourteen than eleven?’” I wrote both questions on the easel.“When we want to find out how much more a number is than another number, we need to compare them. How could we compare the amounts fourteen and eleven?”
“We could look on the hundreds chart. See, there is eleven and a few spaces away is fourteen,” Martha suggested, pointing to the chart.
“How many spaces away is fourteen from eleven?”
Martha walked up to the chart and put her finger on 11, then counted over to 14. “One, two, three,” Martha said as she touched 12, 13, and 14 on the hundreds chart.
“So fourteen is three more than eleven. I wonder if we can start from fourteen and count back to eleven. Lucy, will you go try?”
Lucy placed her finger on 14 and said, “One.” She moved her finger to 13 and said, “Two.” Then she said, “Three,” as she placed her finger on 12. When she landed on 11, she said,“Four.” Lucy turned around with a confused look. I decided to get the cubes out to help Lucy and others make sense of counting on and counting back. I knew I could tell her that we don’t start counting on the starting number, but I also realized she may not know why and needed to see a concrete example to help her.
I placed fourteen Snap Cubes in the middle of the rug and said, “Fourteen.” Then I removed one and said to the class, “Tell me how many are in the pile.”
The whole class chimed in, “Thirteen!”
I pointed to the hundreds chart and explained, “When our finger is on fourteen, that represents the whole group of fourteen Snap Cubes you see in the floor.” I asked someone to explain what I did next.
“You moved one over so that we have thirteen,” said Marcus.
“When I moved one away from the pile, it was the same as moving one finger over to thirteen and saying, ‘One.’ We are counting how many we just took away to get closer to eleven. Let’s continue until we get to eleven.” I stayed at the hundreds chart and asked Marcus to take another cube away.
“How many are in the pile now?”
“Twelve,” the whole class said in unison. I moved my finger over to 12. “So far, how many cubes have we taken out of the pile?”
“Two!”
“And how many spaces have I moved?” “Two!”
Marcus took one more cube and I moved my finger one more time to 11.
The class said, “Three.”
“When I moved my finger, it was the same as when Marcus took one cube from the pile,” I restated. I knew that I would need to revisit the idea of counting on or counting back for some students. “So, can we count back to figure out how much more fourteen is than eleven?”
“I want to try it again!” Lucy volunteered. She walked up to the hundreds chart and started on 14, then moved to 13 and said, “One.” She continued until her finger landed on 11, at which point she said, “Three.”
“I think you can count back,” Lucy said, still seeming uncertain.
“Yeah, you can. Eleven and fourteen are in the same place. You can go forward or backward and they don’t move,” Maria explained. She seemed a little impatient about the amount of time we were spending counting back. I knew it was time to move on for some kids and made a mental note to work with Lucy on counting back and counting up.
“How else can we figure out how much more fourteen is than eleven?” I inquired.
“We could put the cubes together and see if fourteen is longer?” Seth suggested.
I ask Seth to snap the fourteen cubes together as I snapped eleven together. We compared them by standing them up on the edge of the easel.
I heard several students saying that fourteen was taller. “How much taller is fourteen than eleven?”
“It has three more cubes.” Seth pointed to the last three cubes in the tower of fourteen.
“If you break those off, then they would be the same,” Edgar chimed in. “You’re right, Edgar, if I broke the three off, they would be equal since both would have eleven cubes. My question is How much more is fourteen than eleven? We have three strategies to help us figure that out.” I labeled a piece of chart paper How Many More? Strategies and wrote down our strategies while summarizing them for the class. “We counted on using the hundreds chart, we counted back using the hundreds chart, and we compared Snap Cube towers. Tomorrow when you play the game, I want you to work on figuring out how many more you have than your partner or how many more your partner has than you.”
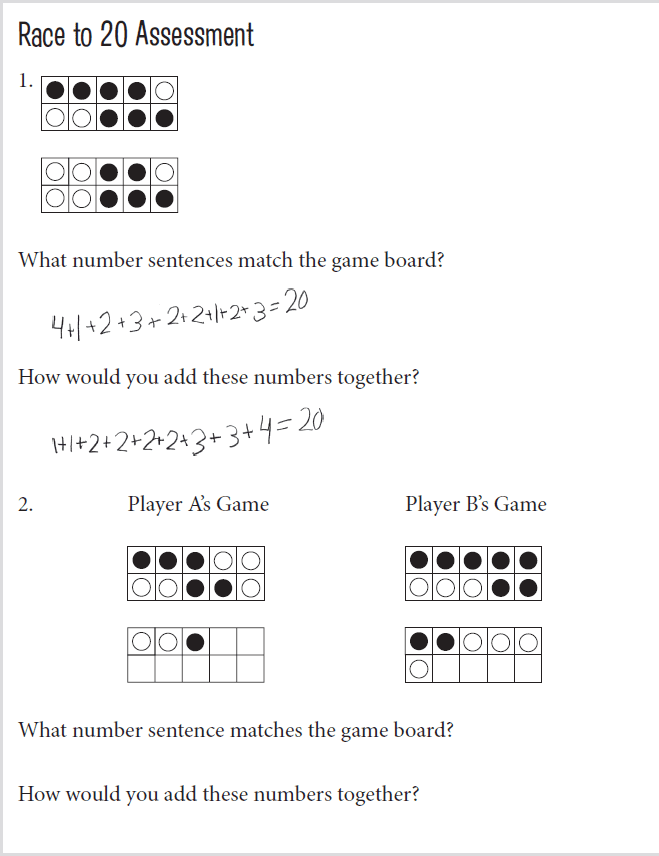
FIGURE G-9.1 Jazzmine rewrote the number string, adding the smaller numbers fi rst, followed by the larger numbers
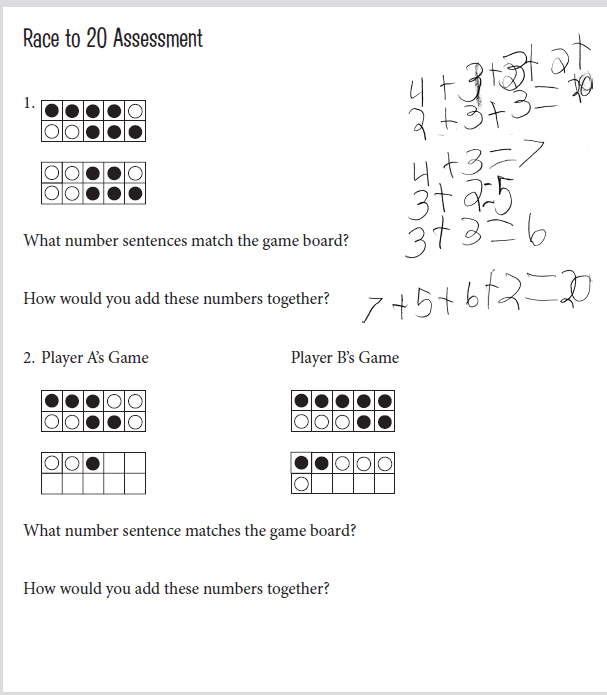
FIGURE G-9.2 Zachary looked for facts he knew

FIGURE G-9.3 For the second round, Emily began by rolling the die

FIGURE G-9.4 Chloe watched as Christian
placed the counters on the ten frame. She then
turned to me and said, “Christian and I both
need five more counters to fill our ten-frame”

Comments