A Fifth-Grade Fractions Lesson

by Kristina Kalb

Kristina Kalb, who teaches gifted third, fourth, and fifth graders in Flemington, New Jersey, is intrigued with the teaching of fractions. This is a lesson she did with her fifth-grade students.

In order to introduce my students to problems that involve division with fractions, I use problem situations that draw on familiar contexts. I keep the focus of their work on making sense of the situation and explaining their strategies and solutions. Some of the problems I use don’t require that students necessarily arrive at a precise answer, but rather allow them to use the information at hand to arrive at a correct solution. In this way, the students’ experiences mirror how we often encounter problems in real life.

For example, I gave my fifth graders the following problem:

I purchased one giant 5 3/4-pound bag of DAJM (Swedish chocolates). I want to separate the candy into 1/2-pound bags to give to my fifth-grade students. How many 1/2-pound bags can I make? Will there be enough for each person in the class? If not, how much more will I need to buy?

By dividing wholes into halves, Jamie solved the problem.

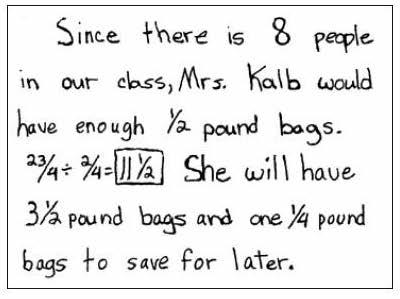
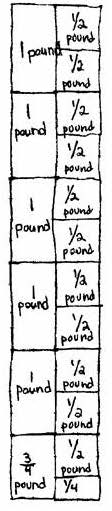
Randy also solved the problem by drawing a picture.

After students shared their answers and the methods they used, I gave them other problems to solve, using other amounts for the sizes of the large and small bags. I didn’t write the chocolate scenario over and over again but presented the situations only with division problems. This helped students connect the original situation to the correct mathematical representation. The problems they solved included the following: 2 2/3 ÷ 1/3 = ? 1 1/2 ÷ 1/4 = ? 1 1/2 ÷ 1/6 = ? 2 5/6 ÷ 1/3 = ? As before, the students were asked to explain the methods they used. The next day, I asked the students to write a word problem to match one of two equations: 1 3/4 ÷ 1/2 = ? or 4 2/5 ÷ 1/3 = ? The problems they wrote helped me assess their ability to connect an equation involving division with fractions to a real-world context.

Here is just a sampling of the problems they wrote:

Tom was buying wood for his woodshop class. Each student needed 1/2 foot of wood to complete his or her project. If Tom buys 1 3/4 feet of wood, how many students can complete their projects? How much wood is left over?

Matt has 4 2/5 candy bars. (Each candy bar has five equal parts.) Matt’s group of friends wants 1/3 of a candy bar each. How many friends can Matt give 1/3 of a candy bar to?

Betty went to the local fabric store for fabric to make curtains. She bought 4 2/5 of a yard. If she needs 1/3 yard to make one curtain, how many curtains could she make? How much fabric is left over?

The students shared their word problems, resulting in some very interesting discussions. After hearing the problem about Betty buying fabric for curtains, for example, I pointed out that if I went to buy fabric to make curtains, I would measure and know ahead of time how much fabric to buy and how many curtains I would be making. However, if I happened to be in the fabric store looking at remnant pieces and found one I liked that was 4 2/5 yards long, I might consider what I could make with it— pillows, aprons, etc.

To follow this experience, I next gave them the assignment to solve the Pinewood Derby problem:

Charles makes Pinewood Derby kits from 8-foot stock. Each model requires a piece of stock that is 7 3/8 inches long. Each cut consumes an additional 1/16 inch of material. How many 8-foot pieces of stock are required to fill an order for 500 kits?

The students understood that they needed to add 7 3/8 to 1/16, and they correctly did that, understanding that one kit needed exactly 7 7/16 inches of wood. After that, no one knew what to do next. I encouraged them to make a model. First they cut out a strip from used file folders that measured 7 7/16 inches long. Then we measured and marked with masking tape 8 feet (or 96 inches) on the classroom floor. At this point, the students were off and running. They carefully measured out 12 pieces of 7 7/16 inches each from 96 inches and then went back to their desks and finished the calculations.