Spaghetti and Meatballs for All!

A Lesson for Fifth and Sixth Graders

Our latest Math By All Means replacement unit, Area and Perimeter, Grades 5–6, is written by Cheryl Rectanus. One whole-class lesson in the book is based on Spaghetti and Meatballs for All!, a children’s book by Marilyn Burns. The book sparks a lesson about arranging tables and chairs to accommodate a large number of diners, a real-life context that helps students link area and perimeter to the world around them.

---

Related Publication:
Spaghetti and Meatballs for All! A Mathematical Story
by Marilyn Burns

Cheryl began the lesson by reading Spaghetti and Meatballs for All! aloud to the class. In the story, Mr. and Mrs. Comfort invite 32 family members and friends for a reunion and set eight square tables to seat four people at each, one to a side. As guests arrive, they all have their own ideas about how to rearrange the tables so that different-size groups can sit together. Mrs. Comfort protests, knowing that there will be seating problems later, but her protests are ignored. The party becomes a cheerful confusion of rearranged tables, chairs, plates, glasses, and food. It all works out in the end, however, when Mrs. Comfort was proved right after all.

When Cheryl finished reading the story, she asked the class, “What was Mrs. Comfort worried about?”

Nicole answered first, “There wasn’t going to be enough room, because when you push tables together you lose chairs,” she said.

“What do you mean?” Cheryl asked.

“It’s like, if you put two tables together, you lose seats where the tables touch. It’s hard to explain.” Nicole drew two tables in the air, pointing to the sides where they met. Cheryl sketched two squares on the board, drawing an arrow where the sides touched. “You mean lose chairs here?” she asked. Nicole nodded. (See figure 1).

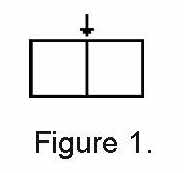
After hearing other students’ ideas about Mrs. Comfort’s problem, Cheryl said, “Let’s use Color Tiles to explore different ways to arrange just four tables. We’ll start with just four tables.”

Cheryl gave the class guidelines for arranging the square “tables.” “When tiles touch,” she said, “they must do so along an entire side. Parts of sides or only corners touching is not okay.” She demonstrated on the overhead projector. (See figure 2.)

 

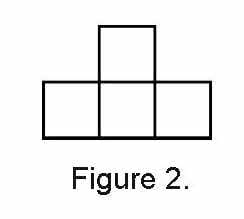
Cheryl also arranged the tiles in a way that didn’t follow her rule and had students explain why. (See figure 3.)

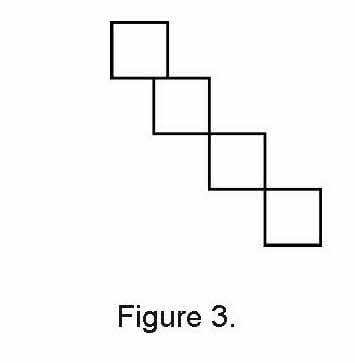
Then she completed the instructions. “In your group, share the tiles I’ve placed on your table and find different ways to arrange four tiles. Be sure to follow my rule.” Cheryl had put out about 70 tiles for each group of four students.

As the students worked, Cheryl circulated around the classroom, observing the students and answering questions as needed. When everyone had had a chance to work on the problem, she interrupted the students and asked for their attention.

“What arrangements did you make?” Cheryl asked. “Who would like to describe an arrangement so I can build it with tiles on the overhead?”

“You can make a straight line,” Brandon reported.

“Like this?” Cheryl asked, arranging four tiles into a 1-by-4 rectangle. Brandon nodded.

“Make a square with all four of them,” Rachel said. Cheryl built a square using four tiles.

“I did a three and a one,” Nicole said.

“What do you mean?” Cheryl asked.

“One little table like one of Nathan’s,” Nicole explained, “and then a 1-by-3.”

“You can make four separate tables,” Nathan said.

“You could make a T,” Zak said. “Put three in a line and one underneath the middle one.”

“I made that too, but mine’s upside down,” said Eric.

Cheryl built Eric’s arrangement under Zak’s and pointed out to the class that when you can flip, rotate, or slide a shape to fit exactly on another shape, the shapes are congruent. “We’ll consider congruent shapes to be the same,” she explained.

When the students’ arrangements filled the overhead, Cheryl asked, “What if the only arrangements we used were single rectangular tables made from four tiles? What shapes should we remove?”

“The four separate tables I suggested,” Nathan said.

Rifka added, “And the one that looks like the letter T.”

“You also have to take off mine,” Nicole said. “It’s not a single rectangle.”

When Malkia suggested removing the square, conversation erupted. Some students remembered that a square was a rectangle, but others didn’t. Cheryl clarified, “A square is a special kind of rectangle because its sides are all the same length. But, like a rectangle, a square still has four 90-degree angles and opposite sides parallel.”

Cheryl wanted to be sure the students had a way to label the rectangles they built. She sketched a 1-by-4 rectangle on the board. “I can record this in two ways,” she said, and recorded under the rectangle:

 

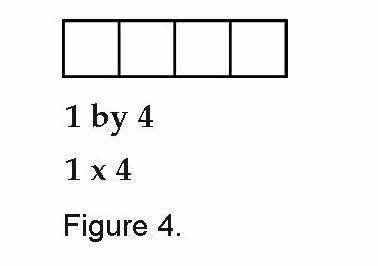
Cheryl then drew a 2-by-2 square and labeled it.

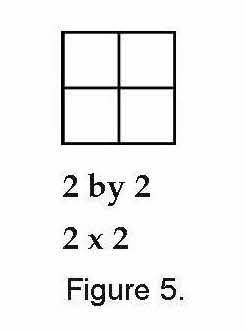
Cheryl pointed to the 2-by-2 square table and asked, “If one person sits on a side of a small square table, and no one sits at the corners or on the cracks between tables, how many people can sit here?”

“Easy, eight,” replied Nicole. “Just count two people on each side times four sides.”

“When you count the number of people who can sit at the table, you’re actually finding its perimeter,” Cheryl explained. “That’s because each person sits at one side of the smaller squares and takes up one unit of length. So the perimeter of the 2-by-2 rectangle is 8 units.”

“The perimeter of the 1-by-4 table is 10,” Eric noticed.

Cheryl had the others check Eric’s statement and also figure the perimeter of several other rectangles. She then introduced another problem.

“Let’s think back to Mr. and Mrs. Comfort’s party,” Cheryl began. “Suppose that Mrs. Comfort had decided that all 32 people should sit at one large, solid rectangular table and she wanted to figure out how many small square tables to rent. See if you can find all the possible rectangular tables of different sizes and shapes that can seat 32 people.”

“Does each table have to fit exactly 32?” JT wanted to know.

“Yes,” Cheryl replied.

“How many tiles do we use?” Malkia asked.

“It will depend on the tables you build,” Cheryl responded.

“Can we work with a partner?” Nicole asked.

“Yes,” Cheryl replied, “but keep your own record.”

There were no more questions. Cheryl gave one last direction. “Use the tiles, but draw your solutions on a piece of paper. Be sure to record the dimensions of each table and the number of people it will seat.”

Observing the Children

For the rest of the class period, Cheryl observed the students at work and gave assistance when needed.

She watched Kathleen make a 16-by-2 rectangle. “Hmm,” Kathleen said aloud as she worked, “let’s see, 32 people. This should work, because 16 times 2 is 32.” Kathleen frowned with concentration as she counted the sides of the squares. Then she looked up at Cheryl in surprise.

“I don’t get it,” she said. “I counted 36 seats. But that doesn’t make sense, because 16 times 2 is 32. Maybe I counted wrong.” She counted the sides again.

“Still 36. Huh.” Kathleen shrugged, mixed the 16 tiles back into the pile in the middle of her table, and began building another rectangle.

“What are you doing?” Cheryl asked her.

“Well, I must have messed up ‘cause the first one I made didn’t work, so I’m going to try something else,” Kathleen replied.

“What are you going to try?” Cheryl asked.

“I don’t know. I’m just going to mess around and see what happens,” she said.

Cheryl watched as Kathleen began placing tiles in a long row one square wide. She kept counting the sides one by one each time she added a new tile. Finally, she smiled.

“It works! This one seats 32 people. It’s a 1-by-15. Now to record it.” Kathleen began sketching the rectangle on her paper.

Alex was sitting across from Kathleen. “I found that one too,” he said. “Now I’m trying a 2-by something.”

“Oh,” Kathleen responded and then began to build a rectangle that was four squares wide.

Nathan came up to Cheryl. “I’m not drawing rectangles on my paper like everyone else,” he said. “I decided to use Xs instead. But Luke told me it was wrong. Can’t I draw Xs if I want to?” Nathan showed Cheryl his paper.

Cheryl asked Nathan to explain what he had done. Satisfied that he understood what he was doing, Cheryl said, “What you’ve done makes sense to me.”

Nathan ran back to Luke. “I told you she’d say it was okay,” he said.

Cheryl continued around the classroom. By the end of the period, she saw that all of the students had found some of the rectangles and some had found them all. She asked the children to put away the tiles and she collected their papers. Cheryl planned to continue the lesson the next day.

The Next Day

The next morning, Cheryl gave the class an extension to consider. “What’s the least expensive way to seat 32 people at one large rectangular table? And what’s the most expensive way? To answer, some of you will need to find more table arrangements.”

After about 10 minutes, Cheryl interrupted the students to begin a class discussion. “What options would the Comforts have to seat all 32 people at one table?” Cheryl asked. Students’ hands shot up.

“They’d have a bunch, eight to be exact,” Rachel said. Most students nodded or murmured their agreement.

“Can someone describe the dimensions of the tables that would work?” Cheryl asked. “I’ll record them on the board.”

Eric reported, “One-times-15, 2-times-14, 3-times-13, 4-times-12, 5-times-11, 6-times-10, 7times-9 and 8-times-8.” After Cheryl recorded the dimensions, she went back and sketched each corresponding rectangle.

“Oh, I see a pattern!” Anfernee said. “Can I show it?” Cheryl nodded, and Anfernee came to the board. She said, pointing, “From the top to the bottom it goes 1, then 2, then 3, then 4, then 5, and so on, up to 8.”

“And the other side goes down,” Ann Maria added.

“Oh, yeah, I didn’t see that,” said Anfernee. “Yeah, 15, 14, 13, and on and on.” He sat back down.

“Shouldn’t the list keep going?” Cheryl asked. “Shouldn’t a 9-by-7 rectangle come next?” (See figure 6.)

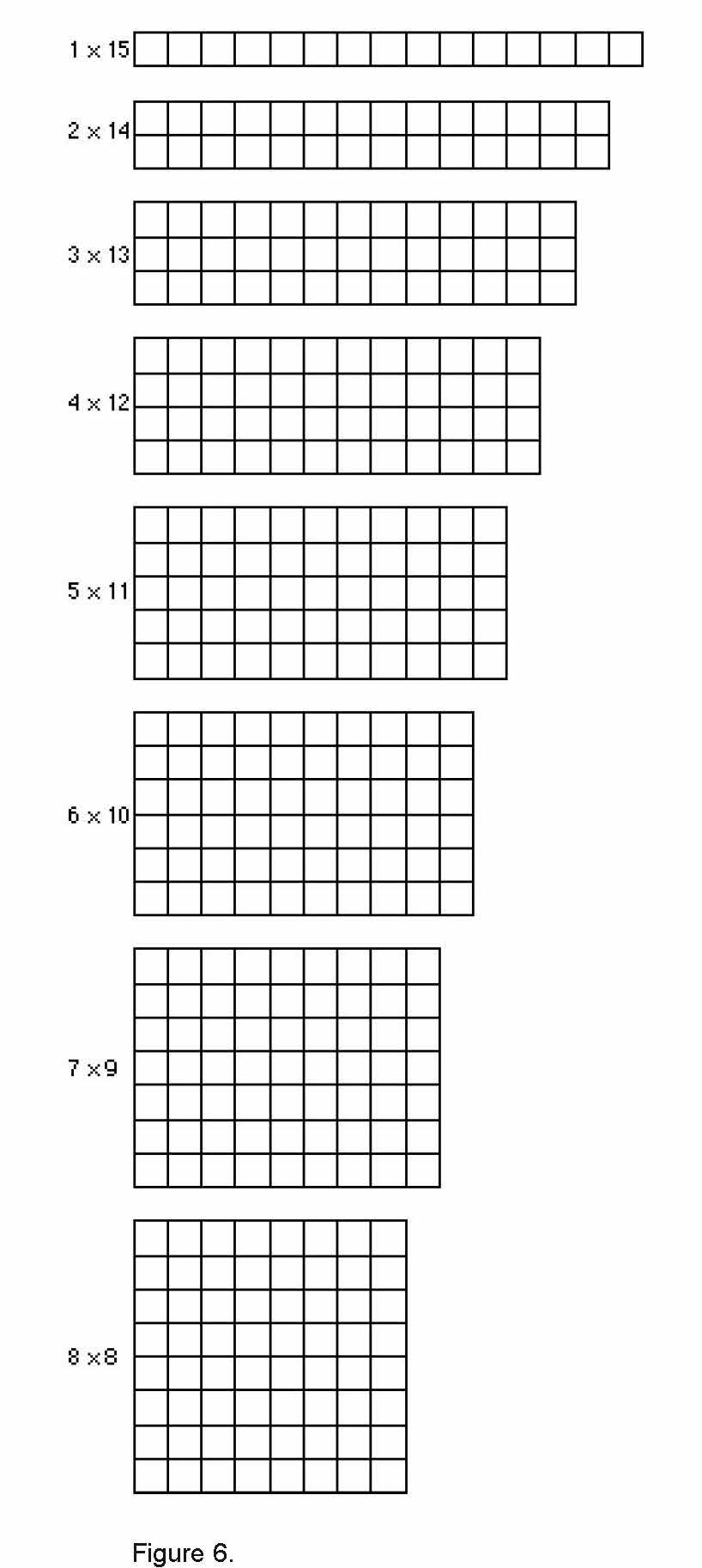
“You’ve got that one already,” Malkia said.

“Yeah, 9-by-7 and 7-by-9 are the same,” Nicole added.

“All the ones after 8-times-8 are repeats,” Kirsten said, “so you can’t count them.”

“Let’s think about how many square tables Mr. and Mrs. Comfort would have to rent for each large rectangle,” Cheryl said. “How many would they have to rent for a 15-by-1 table?”

“Fifteen. Easy,” several students responded.

“What about 2-by-14?” Cheryl continued. “How many tables would the Comforts have to rent for that arrangement?”

“Twenty-eight,” many children called.

“What about the 3-by-13 arrangement?” Cheryl asked. The class quickly caught on to what Cheryl was doing.

“You’re just multiplying,” Rifka said. “Just do that for all of them – 28, 39, 48, 55, 60, 63, and 64.”

“What do you notice about the shapes of the tables?” Cheryl then asked.

Malkia said, “The 8-by-8 is a square, and all the rest are rectangles.”

“But the 8-by-8 is a rectangle too, remember?” Erin reminded Malkia.

“Look,” Brandon said. “If they arrange a long, skinny rectangle for 32, then they can do it with only 15 tables. It’s cheapest that way.”

“And they’d save space, too, since the 1-times-15 takes up the least amount of space,” added Sharnet.

“You’d need a long room, though,” Nicole added, “like for a king’s banquet.”

Cheryl then stopped the conversation and gave a writing assignment to assess each student’s thinking. She wrote three questions on the board for the children to answer:

1. What patterns were useful as you worked?
2. What table arrangements are the most and least economical?
3. What do you notice about the areas and perimeters of the arrangements you made?

The students worked on the assignment for the rest of the class.